最大似然估计与最大后验概率估计
最大似然估计与最大后验概率估计
两大学派
频率学派
- 认为:世界是确定的 ==> 可以通过某种方式对事件进行建模
- 建模方法:MLE, max likelihood estimate
贝叶斯学派
- 认为:世界是不确定的,同一个事件由于观测/假设的不同而不同 ==> 无法直接对事件进行确定性的唯一建模 ==> 先假设一个先验,利用先验得到后验 ==> 推断先验的分布
- 建模方法:MAP, max a Posteriori estimation
MLE
- 似然:观测到了结果 ==> 假定结果服从一个分布(例如画图发现服从高斯分布,但不知道具体的分布参数),估计最有可能出现这些结果的分布参数。
- 对观测到的数据X,假定其服从某个分布,并设该分布的参数为θ,求p(X | θ)最大时的θ值。
- MLP的前提认为当前观测得到的样本独立同分布,且与总体的分布一致。所以观测到的结果越多,估计越准。
- 似然函数:L(θ | X) = p(X | θ)。假设n个随机变量x1, … , xn独立同分布。则:
- 最大似然时得到的参数即为MLE估计的参数
- 一般取log似然
- 连乘 —> 连加:不易下溢/上溢;方便求解。
- MLE求解时,核心是需要写出p(X | θ)。ML中,模型参数会转化为某个分布的参数,并利用MLE求解。例如f(x)=wTx+b,假设其噪声服从e~N(0, σ2),则f(x)~N(wTx, σ2),接下来就可以利用MLE求解w了。
MAP
- 先验:假设θ服从某个分布g(θ)
- 而MLE中假设θ的值是确定的某个分布的参数
- MLE可以看作先验为常数分布的特殊MAP;MAP可以看作对MLE估计的一个校正。
- 后验:观察到某些样本的条件下,先验的分布。后验概率 := 似然概率*先验概率。
- MAP在先验假设下估计得到的参数仍然是一个确定的值,而当样本量无限大,P(θ)的作用越来越小。
- 即数据量无限大时,先验假设的影响可以忽略不计。
- 数据量无限大时,MAP := MLE
Case
Case1
- 假设有一个罐子,罐子里面有黑白两种球,数目未知。每次任意从罐子里面取一个球,记录颜色,放回罐子里面。重复 10 次,假设 7 次白球,3 次黑球,那么罐子里面白球的比例最有可能是多少?
MLE
由于只有两种颜色的球,可以假设白球的概率服从二项分布(模型已知)。假设白球概率为θ,黑球为1-θ。按照最大似然估计,似然函数为:
-> log -> argmax —> p = 0.7
MAP
先验:假设p~N(0.5, 0.1)
带入μ=0.5,σ=0.1 —> log —> 求argmax —> θ = 0.66349
而当试验次数达到1000次,700次正例的话 θ = 0.69958
Case2-MSE Loss
- 用MLE推导MSE Loss
- 每个样本i可以表示为 , 此处可以简单表示为, 原因是
- Loss在形式上是 和 的函数
- 每个样本i可以写为 ,因此可以认为的表示中已经包含了x_i
机器学习算法需要学习的是整体分布y’,而样本是y1…yn,假设每个样本与其整体分布的误差e为一个正态分布,即
L(y’ | y) = p(y1…yn | y’1…y’n)
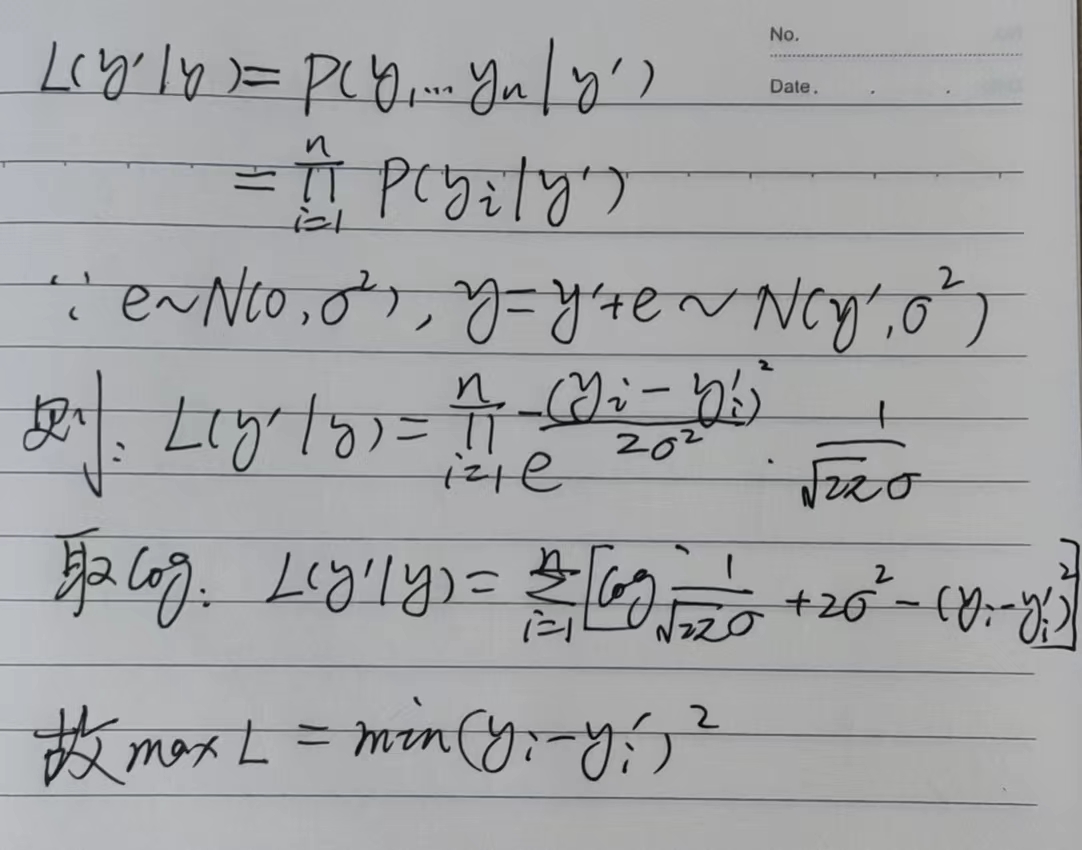
Case3-Log Loss
- 用MLE推Log Loss
