计组-原码、反码、补码、移码、浮点数、校验码

Posted on Edited on In ,

ref

码制-原码、反码、补码、移码

  • 原码：符号位+数值位。直观，但是运算较为困难，加法和减法需要采取不同的硬件实现方式；0有+0和-0两种表达方式。
  • 反码：正数的反码：原码，负数的反码：原码的数值位取反。0有+0和-0两种表达方式
  • 补码：正数的补码：原码，负数的补码：反码数值位+1。能将减法运算转换为加法运算，使得加减法能采用同一套硬件实现；0的表示唯一
  • 移码：补码的符号位取反（不区分正负数）。和补码一样，方便运算；且整体大小单调递增，用于表示浮点数的阶码；0的表示唯一

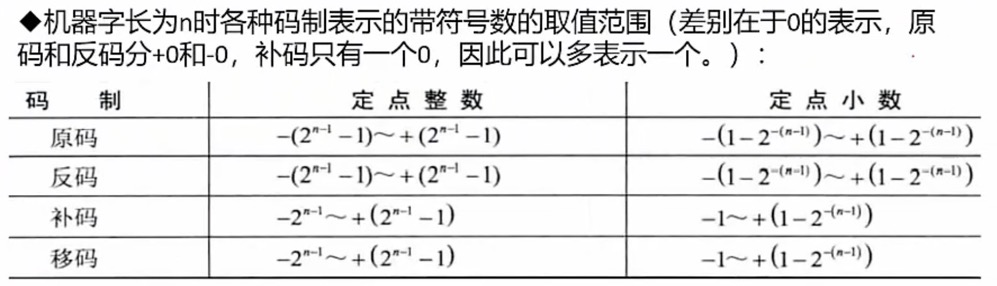
表示范围

  • 原码和反码一样，补码和移码一样。后者比前者在负数上多表示一个数，原因是前者的0有两种表达方式。
  • 从0开始，因此最大值都要减一
  • 小数是对整数都除以2^(n-1)

规格化

  • 对于规格化浮点数小数点后第一个值是固定的（正数：1，负数：原码1，补码0）
  • 目的：为了提高精度需要使尾数的有效位数尽可能占满可用的位数。这种措施称为浮点数的规格化。
  • ref

浮点数

  • 浮点数在计算机中的表示
    • 浮点数表示时，尾数使用纯小数(有的是0.xxx的小数，有的是1.xxx的小数)
1
2
3
4
5
|<-----j-------->|<--------S-------->|
+----|-----------|----|--------------+
| jf | j1j2...jm | Sf | S1S2...Sn    |
+----|-----------|----|--------------+
 阶符     阶码     数符 |    尾数数值
  • 例如-28.75，用1位阶符、5位阶码、1位数符、8位尾数，阶码和尾数都采用原码表示，则可以表示如下：
    1
    2
    3
    4
    5
    6
    (-28.75)base10 
    = (-110100.11)base2
    = -1 * (0.11010011)base2 * 2^5
    阶符 jf = 0， 阶码 j1j2j3j4j5 = 00101 = 5， 数符 Sf = 1， 尾数 S1S2...S8 = 11010011
    结果：
        0 00101 1 11010011

表示范围

  • 先确定阶码位和尾数位是用什么码制表示。尾数的最大最小值分别和阶码最大值相乘即可。
  • IEEE-754
    • 尾数的规格化方式：省略了开头的“1.”，即M表示的是1.M
    • 阶码表示以2为底的阶数，用移码表示，但需要注意的是，这里的移码不能采取将补码的最高位取反的方式获得，这是因为把补码的最高位取反，相当于增加了1000…00的偏置量，而IEEE 754标准下的偏置量是0111…11，也就少了一个1。之所以这样设计，是为了保留阶码全0或者全1的情况，以用作特殊用途。
    • 因此，以float型浮点数转化为十进制数的计算公式为：
1
2
3
4
+------|-----------------------|----------------------+
|   S  |     阶码J（含阶符）     |       尾数M          |
+------|-----------------------|----------------------+
  数符       （采用移码）        |     （采用原码）

浮点数运算

校验码

  • 码距/海明距离：任意两个码字之间最少变化的二进制位数

奇偶校验码

  • 分奇校验和偶校验
  • 预留一位作为校验位，以奇校验为例，值为1则说明有奇数个1，反之有偶数个1
  • 只能检错不能纠错、且只能检验出奇数个数据改变的场景

海明校验码

  • 一种多重奇偶校验码。
  • 实现原理：在有效信息位中加入几个校验位形成海明码，并把海明码的每一个二进制位分配到几个奇偶校验组中。当某一位出错后，就会引起有关的几个校验位的值发生变化。
  • 特点：可以发现错误，定位错误位置，自动纠正错误。 可以检测双比特错误，但只能纠正单比特错误。

    纠错理论：L-1=D+C且D≥C：编码最小码距L越大，其检测错误的位数D越大，纠正错误的位数C也越大，且纠错能力恒小于检错能力

  • case

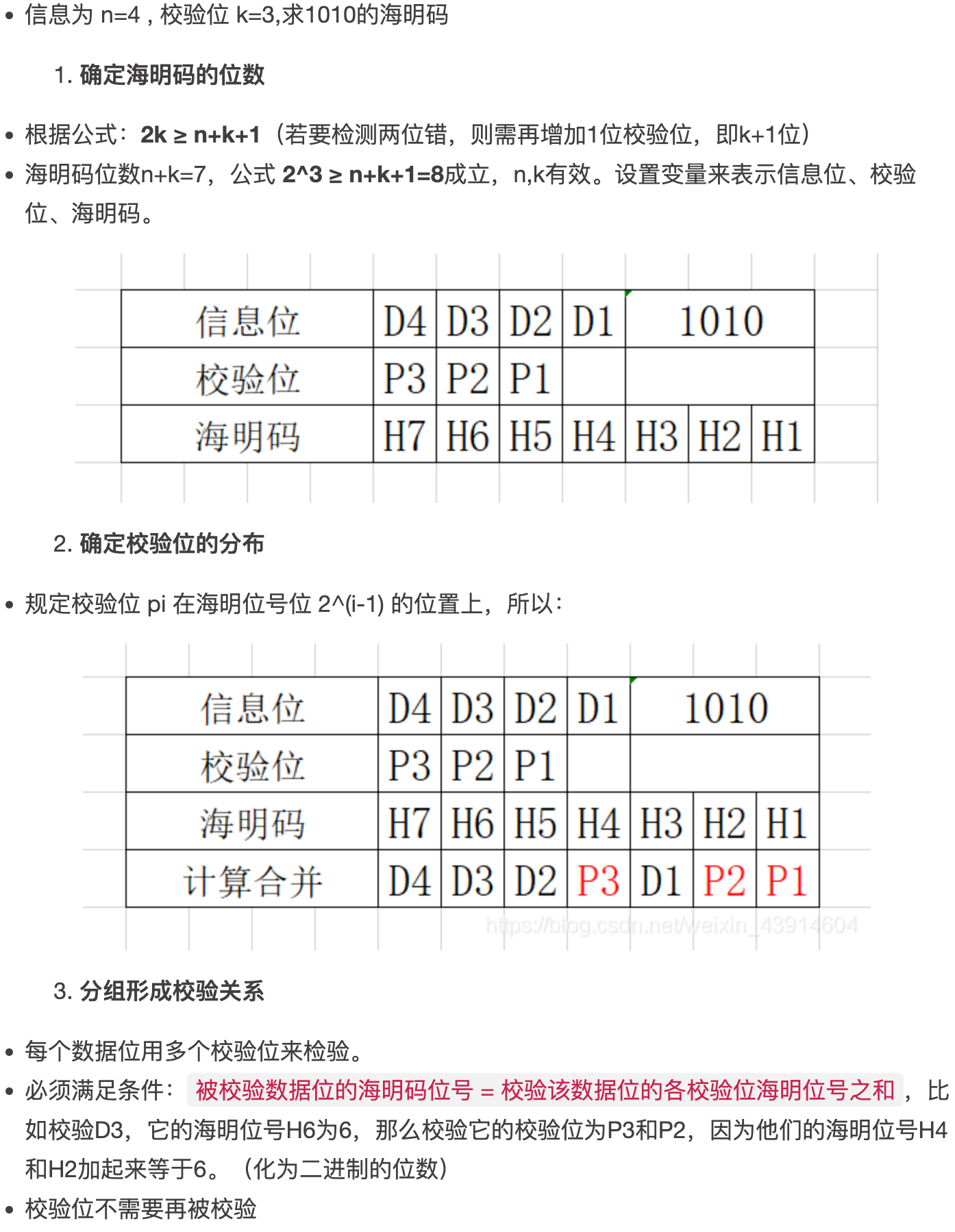
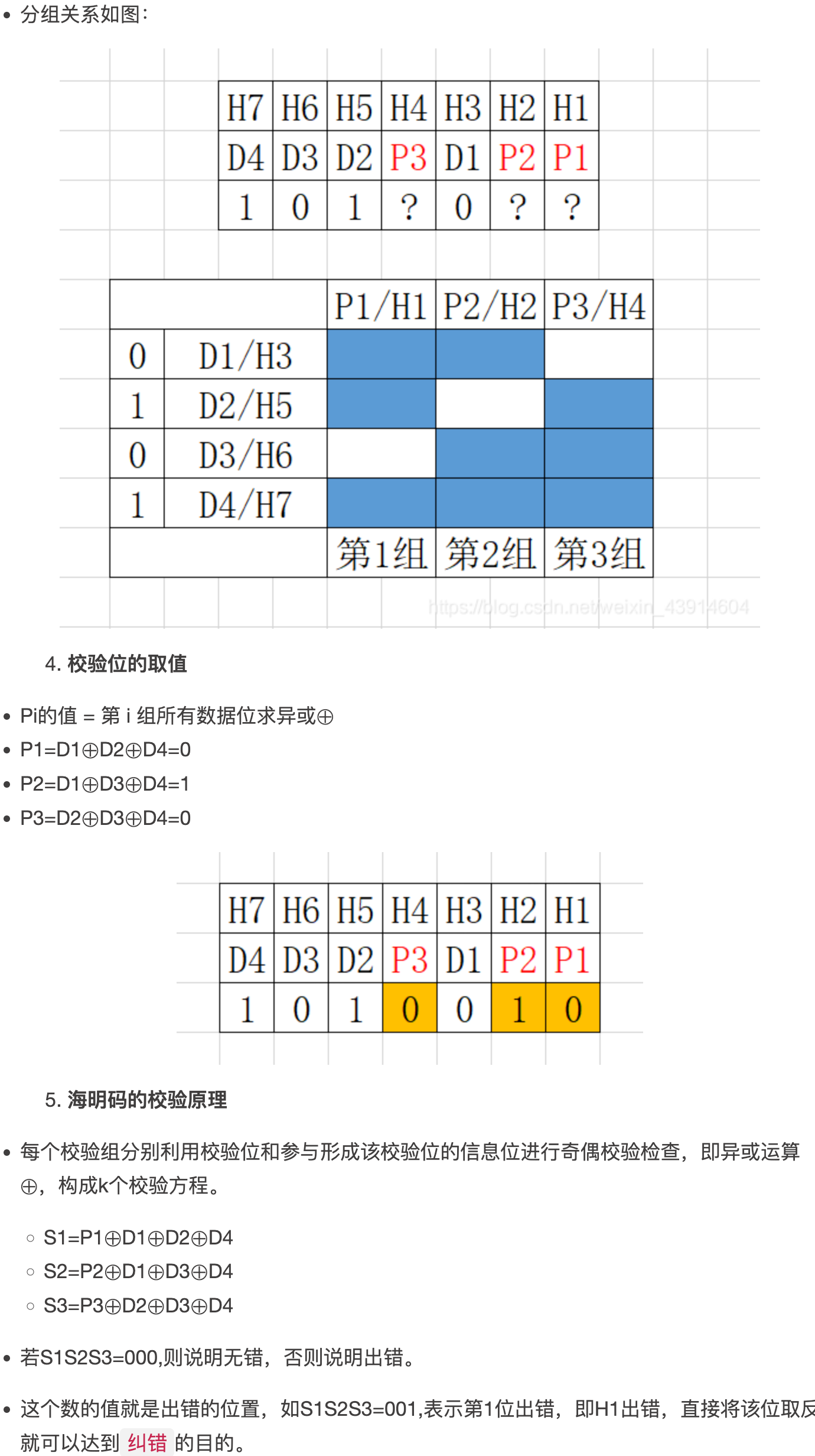
hammingcode1.png

循环冗余校验码（Cyclic redundancy check, crc）

  • CRC码共N位：K位信息位后拼接R位校验码。K+R=N，也称(N,R)码。
  • 可以发现错误，定位错误位置，自动纠正错误。可检测/纠正出所有奇数位错，所有双比特的错和所有小于、等于校验位长度的突发错
    1. 发送端和接受端会有一个生成多项式G(x)约定,生成多项式G(x)的最高次幂为R。任意一个二进制数码都可用一个系数为0或1的多项式与之对应。比如：二进制数码 1101 对应的G(x)=1X^3+1X^2+0X^1+1X^0= X^3+X^2+1
    1. 在发送端，将要传送的K位二进制信息码左移R位，将它与生成多项式G(x)所对应的的二进制数码进行模2除法（按位异或），产生余数，生成一个R位检验码，并附在信息码后，构成一个新的二进制码（CRC）码，共K+R位。
  • case

存储系统 & 存储管理

存储结构

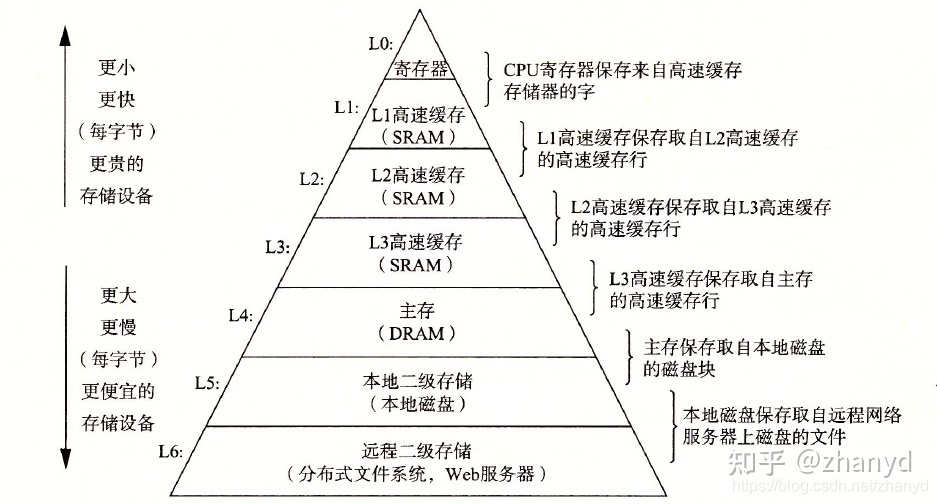
  • 存储器层次结构的思想是上一层次的存储器是低一层次的高速缓存。
  • 越接近cpu的存储器速度越快容量越小，越远离cpu的存储器速度越慢容量越大。
  • 高速缓冲技术是利用程序访问的局部性原理，把程序中正在使用的部分存放在一个高速的、容量较小的Cache中，使CPU的访存操作大多数针对Cache进行，从而大大提高程序的执行速度。

局部性原理

  • 空间局部性：一个存储位置被访问后，其周围的位置也倾向于被访问。
  • 时间局部性：一个存储位置倾向于被多次访问（类似循环体中的变量）。
  • 程序越满足局部性，其执行效率越高。例如GRU的缓存机制利用了时间局部性，prefetch利用了空间局部性的思想。

cache置换算法

  • 随机算法：几乎没意义
  • 先进先出：一定意义
  • 近期最少使用 least recently used : lru 使用最广泛，把数据加入一个链表中，按访问时间排序，发生淘汰的时候，把访问时间最旧的淘汰掉。。利用hash表（实现O(1)的访问）和双向链表（实现O(1)的add/delete）。
    • 查询某个key，没有则返回-1，有则返回，并移动到链表头。
    • 新增某个元素，新增在链表头，若链表满，delete链表尾的元素。
    • LRU对于循环出现的数据，缓存命中不高。例如1，1，1，2，2，2，3，4，1，1，1，2，2，2…..
  • 最不经常使用页置换 least frequently used : 把数据加入到链表中，按频次排序，一个数据被访问过，把它的频次+1，发生淘汰的时候，把频次低的淘汰掉。
    • lfu 问题在于可能前期用的多，后期不用，就会占住内存不释放。LFU对于交替出现的数据，缓存命中不高，例如1，1，1，2，2，3，4，3，4，3，4，3，4，3，4，3，4……

存储管理