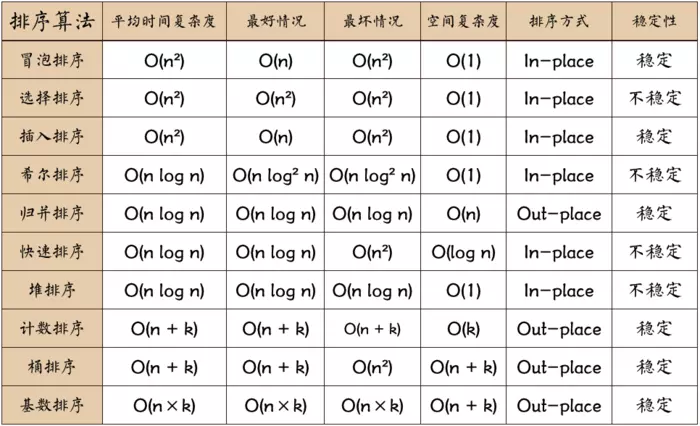
排序算法

Posted on Edited on In

经典排序算法

  • 下文中的稳定是指：若a=b，而排序后的ab顺序与原来的ab顺序一样
  • 交换排序：冒泡、快排；
  • 选择排序：选择、堆；
  • 插入排序：插入、希尔；
  • 归并排序、基数排序

冒泡排序

  • 迭代n-1次，两个相邻元素两两相比，每次迭代将最大的元素放在该迭代序列的顶端。
  • 稳定
  • 优化后，对于最优的情况，即已经正序排列的，算法复杂度为O(N)
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    def bubble_sort(num):
        for i in range(len(num)-1):
            flag = 0
            for j in range(len(num)-i-1):
                if num[j] > num[j+1]:
                    num[j], num[j+1] = num[j+1], num[j]
                    flag = 1
            if flag == 0:
                return num
        return num

选择排序

  • 迭代n-1次，每次选择出最小的，并将最小位置处的值与当前位置值交换
  • 不稳定，因为选择出最小的之后会跟原有数交换顺序，因此会破坏原来的顺序，例如5 3 5 2，第一次之后为2 3 5 5，此时5跟5的顺序变了
    1
    2
    3
    4
    5
    6
    7
    8
    def select_sort(num):
        for i in range(len(num)-1):
            min_index = i   
            for j in range(i,len(num)-1):
                if num[j+1] < num[min_index]:
                    min_index = j+1
            num[i], num[min_index] = num[min_index], num[i]
        return num

    插入排序

  • 插入排序如同打扑克一样，每次将后面的牌插到前面已经排好序的牌中。
  • 最快情况是O(N)，如果大部分数据已经排好序了，while pre_index >= 0 and cur_num < num[pre_index]这句的迭代次数会大大减少，会比较快
  • 稳定
    1
    2
    3
    4
    5
    6
    7
    8
    9
    def insert_sort(num):
        for i in range(len(num)-1):
            pre_index = i # 前一个数
            cur_num = num[i+1] # 当前待插入数 
            while pre_index >= 0 and cur_num < num[pre_index]:
                num[pre_index+1] = num[pre_index] # 往后挪一位，前面的已经排好序了
                pre_index -= 1   
            num[pre_index+1] = cur_num
        return num

希尔排序

  • 对插入排序的优化，使用了递减的增量序列
  • 如上所述插入排序中：如果大部分数据已经排好序了，while pre_index >= 0 and cur_num < num[pre_index]这句的迭代次数会大大减少，会比较快 –> 所以希尔排序就是针对这个做了优化，即先减少需要排序的数量，再逐步对其排序
  • 希尔排序是不稳定的算法，它满足稳定算法的定义。对于相同的两个数，可能由于分在不同的组中而导致它们的顺序发生变化。
  • 希尔排序的性能根据其选取的序列而变化
  • 不稳定
  • 使用动态增量序列的代码如下：
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    def shell_sort(num):
        gap = 1
        while gap < len(num) // 3: #gap < (3a,3a+1,3a+2)//3: (a-1)*3+1=3a-2
            gap = gap*3 + 1
        while gap > 0:
            for i in range(gap,len(num)):
                cur_num = num[gap]
                pre_index = i-gap
                while pre_index >= 0 and cur_num < num[pre_index]:
                    num[pre_index+gap] = num[pre_index] 
                    pre_index -= gap
                num[pre_index+gap] = cur_num
            gap //= 3

归并排序

  • 分治
  • 递归
    • 终止条件：剩一个元素时，返回该元素；再上一层对返回的两个元素比较排序
  • 稳定
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    def merge_sort(num):
        def merge(left,right): # left和right本身是已经排序好的
            result = []
            i=j=0
            while i < len(left) and j < len(right):
                if left[i] <= right[j]:
                    result.append(left)
                    i+=1            
                else:
                    result.append(right)
                    j+=1
            result = result + left[i:] + right[j:]
            return result

        if len(num) <= 1:
            return num
        mid = len(num) // 2
        left = merge_sort(num[:mid])
        right = merge_sort(num[mid:])
        return merge(left,right)

快速排序

  • 冒泡+二分+分治
  • 核心：每次迭代使选取的基准值插入到序列中，该序列中基准值左边的值小于基准值，右边的值大于基准值，然后再对两边分别迭代
  • 基准数选择以及指针移动顺序：最终两个指针相遇时，要把基准数和相遇的位置交换，此时该位置左边的数小于基准数，右边大于基准数；若选择最左边的数为基准数，肯定要跟比它小的数交换，因此只有右指针先动才能找到比它小的（例如算法2里右指针相遇时找到的一定是上一轮左指针的交换结果，一定是小于基准数的）
  • 与归并的区别：
    • 归并是二分，再递归——快排是找到pivot后冒泡，再递归
    • 归并是out-place，快排是in-place
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
## 二分之后不断地递归，每次递归求出基准值的具体位置
def quick_sort1(num):
    if len(num) <= 1:
        return num
    pivot = num[0]
    left = [num[i] for i in range(1,len(num)) if num[i] <= pivot]
    right = [num[i] for i in range(1,len(num)) if num[i] > pivot]
    return quick_sort1(left) + pivot + quick_sort2(right)

def quick_sort2(num,left,right):
    if left >= right: # 两指针相遇，则终止
        return
    low = left
    high = right
    pivot = num[left]
    while left < right:
        while left < right and num[right] > pivot:# 因为记录了left，所以要从right开始
            right -= 1
        num[left] = num[right]
        while left < right and num[left] <= pivot:
            left += 1
        num[right] = num[left]
    num[right] = pivot        

    quick_sort2(num, low, left-1)
    quick_sort2(num, right+1, high)

def quick_sort3(num,left,right):
    if left < right:
        p = partition(num, left, right)
        quick_sort3(num, left, p-1)
        quick_sort3(num, p+1, right)
    
def partition(num, left, right):
    pivot = num[right] # 这里是从左边开始移动指针的，因此是right
    i = left - 1
    for j in range(left, right):
        if num[j] <= pivot:
            i += 1
            num[i], num[j] = num[j], num[i]
    num[i+1], num[right] = num[right], num[i+1] # 把基准数移过来
    return i+1

堆排序

  • 利用堆进行选择排序
  • 大根堆：根节点的值大于叶子结点的值。用于升序排列。
  • 小根堆：根节点的值小于叶子结点的值。用于降序排列。

排序流程

  • 以大根堆排序为例：
    • 1）先构建大根堆
    • 2）将堆顶元素与原序列最后一个元素交换
    • 3）排除最后一个元素，堆的尺寸减1，更新大根堆
    • 4）重复1~3，直到序列有序

堆的构造：

  • 堆是一个完全二叉树，可以用数组来表示。例如a可以表示为[99,66,45,33,37,10,22,13]，所以对于i处的节点，其子节点坐标为2*i+1, 2*i+2
  • 在构造最大堆时，可以先构造一颗完全二叉树，再对每个根节点及其两个子节点进行位置调整，在调整时，从最后一个非叶子节点开始调整
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def adjust_heap(nums, i, size): 
    '''
    nums[:size]: 完全二叉树
    i: 从第i个节点开始调整直到根节点
    '''
    left = 2*i+1
    right = 2*i+2
    largest = i
    if left < size and nums[largest] < nums[left]: # 要保证小于size
        largest = left
   if right < size and nums[largest] < nums[right]:
        largest = right
   if largest != i: # 如果该节点需要调整，则对其进行调整，并沿着被改变的那个叶子节点不断调整
        nums[largest], nums[i] = nums[i], nums[largest]
        adjust_heap(nums, largest, size)

def build_heap(nums):
    for i in range(len(nums)//2)[::-1]: #从最后一个非叶子结点开始调整，往上的节点都是非叶子结点
        adjust_heap(nums, i, len(nums))      

def heap_sort(nums):
    build_heap(nums) # 先建size大小的堆
    size = len(nums)
    for i in range(size)[::-1]:
        nums[0], nums[i] = nums[i], nums[0] #最后的元素一定小于堆顶元素，把堆顶元素放在最后
        adjust_heap(nums, 0, i) # 堆顶元素被改变，需要调整
    return nums

复杂度分析

  • 需要做n次循环，每次从根节点调整堆，并且沿着其中一个子树往下调整，因此为nlogn

计数排序

1
2
3
4
5
6
7
8
9
10
11
def count_sort(nums):
    bucket = [0]*len(max(nums)+1)
    for num in nums:
        bucket[num] += 1
    i = 0
    for j in range(len(bucket)):
        while bucket[j]:
            bucket[j] -= 1
            nums[i] = j
            i+=1
    return nums

桶排序

  • 计数排序的升级版：计数排序每个桶为值本身即y=x，桶排序加了一个映射关系，即y=f(x).该映射关系应做到：在额外空间充足的情况下，尽量增大桶的数量
  • 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中
  • 什么时候最快（Best Cases）：当输入的数据可以均匀的分配到每一个桶中
  • 什么时候最慢（Worst Cases）：当输入的数据被分配到了同一个桶中
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    def bucketSort(nums, defaultBucketSize = 5):
        maxVal, minVal = max(nums), min(nums)
        bucketSize = defaultBucketSize  # 如果没有指定桶的大小，则默认为5
        bucketCount = (maxVal - minVal) // bucketSize + 1  # 数据分为 bucketCount 组
        buckets = []  # 二维桶
        for i in range(bucketCount):
            buckets.append([])
        # 利用函数映射将各个数据放入对应的桶中
        for num in nums:
            buckets[(num - minVal) // bucketSize].append(num)
        nums.clear()  # 清空 nums
        # 对每一个二维桶中的元素进行排序
        for bucket in buckets:
            insertionSort(bucket)  # 假设使用插入排序
            nums.extend(bucket)    # 将排序好的桶依次放入到 nums 中
        return nums

基数排序

  • 桶排序的推广
  • 基数排序是桶排序的一种推广，它所考虑的待排记录包含不止一个关键字。例如对一副牌的整理，可将每张牌看作一个记录，包含两个关键字：花色、面值。一般我们可以将一个有序列是先按花色划分为四大块，每一块中又再按面值大小排序。这时“花色”就是一张牌的“最主位关键字”，而“面值”是“最次位关键字”。
  • 基数排序有两种方法：
    • MSD （主位优先法）：从高位开始进行排序
    • LSD （次位优先法）：从低位开始进行排序

      LSD Radix Sort

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      def radixSort(nums):
          mod = 10
          div = 1
          mostBit = len(str(max(nums)))  # 最大数的位数决定了外循环多少次
          buckets = [[] for row in range(mod)] # 构造 mod 个空桶
          while mostBit:
              for num in nums:  # 将数据放入对应的桶中
                  buckets[num // div % mod].append(num)
              i = 0  # nums 的索引
              for bucket in buckets:  # 将数据收集起来
                  while bucket:
                      nums[i] = bucket.pop(0) # 依次取出
                      i += 1
              div *= 10
              mostBit -= 1
          return nums

大数据排序

  • top k/ bottom k/ 中位数：堆
  • 排序：bitmap
  • 去重：bitmap

堆

  • 作用：求前n大（top k)，前n小，中位数
  • 前n大：维护一个size为n的最小堆，当有新的元素时，与堆顶元素比较，若比堆顶元素大，则替换堆顶元素
  • 前n小：维护size为n的最大堆
  • 问题实例：100w个数中找最大的前100个数。用一个100个元素大小的最小堆即可。

Bitmap

  • 用一位代表一个数字
  • 例如N=10000，则需要使用int a[9999//32 + 1]的内存，因为python的int默认是符合数，所以第一位不能用，- 则数组个数为(N-1)//31+1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# -*- encoding:utf-8 -*-
class Bitmap():
    def __init__(self,max):
        '确定所需数组个数'
        self.size = int ((max + 31 - 1) / 31)
        self.array = [0 for i in range(self.size)]

    def bitindex(self,num):
        '确定数组中元素的位索引'
        return num % 31

    def set_1(self,num):
        '将元素所在的位 置1'
        elemindex = num // 31
        byteindex = self.bitindex(num)
        ele = self.array[elemindex]
        self.array[elemindex] = ele | (1 << byteindex)

    def test_1(self,i):
        '检测元素存在的位置'
        elemindex = i / 31
        byteindex = self.bitindex(i)
        if self.array[elemindex] & (1 << byteindex):
            return True
        return False
if __name__ == '__main__':
    Max = ord('z')
    suffle_array = [x for x in 'qwelmfg']
    result = []
    bitmap = Bitmap(Max)
    for c in suffle_array:
        bitmap.set_1(ord(c))
    for i in range(Max+1):
        if bitmap.test_1(i):
            result.append(chr(i))
    print u'原始数组为:    %s' % suffle_array
    print u'排序后的数组为: %s' % result

外部排序

外部排序基础步骤

  • 两个步骤：
    • 1）将需要排序的文件多次读入内存进行排序，并写入到多个文件里；
    • 2）多路归并
  • 例如：2路归并，每次归并后，可以使m个归并段变为m/2(取上界)个归并段。在实际归并的过程中，由于内存容量的限制不能满足同时将 2 个归并段全部完整的读入内存进行归并，只能不断地取 2 个归并段中的每一小部分进行归并，通过不断地读数据和向外存写数据，直至 2 个归并段完成归并变为 1 个大的有序文件。

败者树/胜者树

  • 与外部排序的性能有关的因素有：k。增加k，会减少外存数据的时间（需要存取的文件变少了），但k的增加会增加内部归并的时间。例如，10个文件，若k=2，则第一次归并时，需要外存5个文件，查找最小值时的归并次数为1；若k=5，则第一次归并时，需要外存2个文件，但内部归并时需要比较4次才能找到最小值。
  • k路归并时使用败者树可以避免k的增加引起的排序效率的降低。
  • 复杂度分析：k路、u个记录、s趟：k个归并段中选取最小的记录需要比较k-1次， 为得到u个记录的一个有序段共需要(u-1)(k-1)次；若归并趟数为s次，那么对n个记录的文件进行外排时，内部归并过程中进行的总的比较次数为 s(n-1)(k-1)，也即(向上取整)(log(k)m)(k-1)(n-1)=(向上取整)(log2m/log2k)(k-1)(n-1)。而(k- 1)/log2k随k增而增因此内部归并时间随k增长而增长了，抵消了外存读写减少的时间，这样做不行，由此引出了“败者树”tree of loser的使用。在内部归并过程中利用败者树将k个归并段中选取最小记录比较的次数降为(向上取整)(log2k)次使总比较次数为(向上取整) (log2m)(n-1)，与k无关。

败者树

  • 胜败：两数相比，小者为胜，大者为败。
  • 败者树和胜者树为一颗完全二叉树。
  • 败者树：其双亲结点存储的是左右孩子比较之后的失败者，而胜利者则继续同其它的胜者去比较。
  • 需要两个数组来表示，内部节点用ls数组，叶子结点为需要排序的序列。
  • 构造过程：
    • a：b3 Vs b4，b3胜b4负，内部结点ls[4]的值为4，表示b4为败者；胜者b3继续参与竞争。
    • b：b3 Vsb0，b3胜b0负，内部结点ls[2]的值为0，表示b0为败者；胜者b3继续参与竞争。
    • c：b1 Vs b2，b1胜b2负，内部结点ls[3]的值为2，表示b2为败者；胜者b1继续参与竞争。
    • d：b3 Vs b1，b3胜b1负，内部结点ls[1]的值为1，表示b1为败者；胜者b3为最终冠军，用ls[0]=3，记录的最后的胜者索引。
  • 重构过程：当b3变为13时，败者树的重构过程如下：
    • a：b3 Vs b[ls[4]],也就是b3 Vsb4,b4胜，继续参加下面的竞争，ls[4]=3记录败者。
    • b：b4Vs b[ls[2]],也就是b4 Vs b0, b0胜，继续参加下面的竞争，ls[2]=4记录败者。
    • c：b0Vs b[ls[1]],也就是b0 Vs b1, b1胜，b1为最终冠军，所以ls[0]=1记录冠军，ls[1]=0记录败者。
  • 败者树简化了重构。败者树的重构只是与该结点的父结点的记录有关，而胜者树的重构还与该结点的兄弟结点有关。所以败者树在外排序的k路平衡归并中使用。

胜者树

  • b3变为11后，重构为：即胜者树在重构时，既需要与父节点比较还要与兄弟节点比较

利用败者树的外部排序算法

  • 1）假设有一个72KB的文件，其中存储了18K个整数，磁盘中物理块的大小为4KB，将文件分成18组，每组刚好4KB。首先通过18次内部排序，把18组数据排好序，得到初始的18个归并段R1~R18，每个归并段有1024个整数。
  • 2）对这18个归并段使用4路平衡归并排序：
  • 第1次归并：产生5个归并段R11 R12 R13 R14 R15
    • 其中R11是由{R1,R2,R3,R4}中的数据合并而来
    • R12是由{R5,R6,R7,R8}中的数据合并而来
    • R13是由{R9,R10,R11,R12}中的数据合并而来
    • R14是由{R13,R14,R15,R16}中的数据合并而来
    • R15是由{R17,R18}中的数据合并而来
    • 把这5个归并段的数据写入5个文件：foo_1.dat foo_2.dat foo_3.dat foo_4.dat foo_5.dat
  • 第2次归并：从第1次归并产生的5个文件中读取数据，合并，产生2个归并段R21 R22
    • 其中R21是由{R11,R12,R13,R14}中的数据合并而来
    • 其中R22是由{R15}中的数据合并而来
    • 把这2个归并段写入2个文件bar_1.dat bar_2.dat
  • 第3次归并：从第2次归并产生的2个文件中读取数据，合并，产生1个归并段R31
    • R31是由{R21,R22}中的数据合并而来
    • 把这个文件写入1个文件foo_1.dat
  • 此即为最终排序好的文件。
  • 其中，归并过程中使用了败者树。

复杂度

  • 共n条记录，对于有m个初始归并段，k路平衡的归并排序，磁盘读写次数为：|log(k)m|
  • 不使用败者树归并：每次需要比较k-1次，则O((n-1)*(k-1))
  • 使用败者树归并：每次需要比较O(log(k))（这个值是每次得到最小值后重构败者树的时间复杂度），即0O((n-1)*log(k))
  • 为啥要乘n-1：每次归并只能产生一个记录，共有n个记录，最后一条记录为最大值

Trie树

结构

  • 1）根节点不包含字符，除根节点外的每一个子节点都包含一个字符。
  • 2）从根节点到某一节点，路径上经过的字符连接起来，就是该节点对应的字符串。
  • 3）每个单词的公共前缀作为一个字符节点保存。

应用

  • 适用范围：数据量大，重复多，但是数据种类小可以放入内存
  • 字符串检索
    • 从根节点开始一个一个字符进行比较：如果沿路比较，发现不同的字符，则表示该字符串在集合中不存在。如果所有的字符全部比较完并且全部相同，还需判断最后一个节点的标志位（标记该节点是否代表一个关键字）。
1
2
3
4
5
struct trie_node
{
    bool isKey;   // 标记该节点是否代表一个关键字
    trie_node *children[26]; // 各个子节点 
};
  • 词频统计
  • 为了实现词频统计，我们修改了节点结构，用一个整型变量count来计数。对每一个关键字执行插入操作，若已存在，计数加1，若不存在，插入后count置1。
    1
    2
    3
    4
    5
    struct trie_node
    {
        int count;   // 记录该节点代表的单词的个数
        trie_node *children[26]; // 各个子节点 
    };

大数据处理相关例题

  • K: 千 2^10
  • M：百万 2&20
  • G：亿 2^30

给定a、b两个文件，各存放50亿个url，每个url各占64字节，内存限制是4G，让你找出a、b文件共同的url？

  • 方案1：可以估计每个文件安的大小为50G×64=320G，远远大于内存限制的4G。所以不可能将其完全加载到内存中处理。考虑采取分而治之的方法。
    • Step1: 遍历文件a，对每个url求取hash(url)%1000，然后根据所取得的值将url分别存储到1000个小文件（记为 a0, a1…a999）中。这样每个小文件的大约为300M。
    • Step2: 遍历文件b，采取和a相同的方式将url分别存储到1000各小文件（记为 a0, a1…a999）。这样处理后，所有可能相同的url都在对应的小文件中，不对应的小文件不可能有相同的url。然后我们只要求出1000对小文件中相同的url即可。
    • Step3: 求每对小文件ai和bi中相同的url时，可以把ai的url存储到hash_set/hash_map中。然后遍历bi的每个url，看其是否在刚才构建的hash_set中，如果是，那么就是共同的url，存到文件里面就可以了。
  • 方案2：如果允许有一定的错误率，可以使用Bloom filter，4G内存大概可以表示340亿bit。将其中一个文件中的url使用Bloom filter映射为这340亿bit，然后挨个读取另外一个文件的url，检查是否与Bloom filter，如果是，那么该url应该是共同的url（注意会有一定的错误率）。

有10个文件，每个文件1G，每个文件的每一行存放的都是用户的query，每个文件的query都可能重复。要求你按照query的频度排序。

  • 方案1：
    • Step1: 顺序读取10个文件，按照hash(query)%10的结果将query写入到另外10个文件（记为 ）中。这样新生成的文件每个的大小大约也1G（假设hash函数是随机的）。
    • Step2: 找一台内存在2G左右的机器，依次对用hash_map(query, query_count)来统计每个query出现的次数。利用快速/堆/归并排序按照出现次数进行排序。将排序好的query和对应的query_cout输出到文件中。这样得到了10个排好序的文件（记为 ）。
    • Step3: 对 这10个文件进行归并排序（内排序与外排序相结合）。
  • 方案2：一般query的总量是有限的，只是重复的次数比较多而已，可能对于所有的query，一次性就可以加入到内存了。这样，我们就可以采用trie树/ hash_map等直接来统计每个query出现的次数，然后按出现次数做快速/堆/归并排序就可以了。
  • 方案3：与方案1类似，但在做完hash，分成多个文件后，可以交给多个文件来处理，采用分布式的架构来处理（比如MapReduce），最后再进行合并。

有一个1G大小的一个文件，里面每一行是一个词，词的大小不超过16字节，内存限制大小是1M。返回频数最高的100个词。

  • Step1: 顺序读文件中，对于每个词x，取hash(x)%5000 ，然后按照该值存到5000个小文件（记为f0,f1,…,f4999） 中。这样每个文件大概是200k左右。如果其中的有的文件超过了1M大小，还可以按照类似的方法继续往下分，知道分解得到的小文件的大小都不超过1M。
  • Step2: 对每个小文件，统计每个文件中出现的词以及相应的频率（可以采用trie树/hash_map等），并取出出现频率最大的100个词（可以用含100个结点的最小堆），并把100词及相应的频率存入文件，这样又得到了5000个文件。
  • Step3: 把这5000个文件进行归并（类似与归并排序）的过程了。

海量日志数据，提取出某日访问百度次数最多的那个IP。

  • Step1：从这一天的日志数据中把访问百度的IP取出来，逐个写入到一个大文件中;
  • Step2：注意到IP是32位的，最多有2^32=4G个IP。同样可以采用映射的方法，比如模1000，把整个大文件映射为1000个小文件;
  • Step3：对于每一个小文件，可以构建一个IP为key，出现次数为value的Hashmap，同时记录当前出现次数最多的那个IP地址;
  • Step4：在这1000个最大的IP中，找出那个频率最大的IP，即为所求。

寻找热门查询：

  • 搜索引擎会通过日志文件把用户每次检索使用的所有检索串都记录下来，每个查询串的长度为1-255字节。假设目前有一千万个记录，这些查询串的重复 读比较高，虽然总数是1千万，但是如果去除重复和，不超过3百万个。一个查询串的重复度越高，说明查询它的用户越多，也就越热门。请你统计最热门的10个查询串，要求使用的内存不能超过1G。
    • (1) 请描述你解决这个问题的思路；
    • (2) 请给出主要的处理流程，算法，以及算法的复杂度。
  • 方案1：采用trie树，关键字域存该查询串出现的次数，没有出现为0。最后用10个元素的最小推来对出现频率进行排序。
    • Step1: 先对这批海量数据预处理，在O(N)的时间内用Hash表完成统计(之前写成了排序，特此订正。);
    • Step2: 借助堆这个数据结构，找出TopK，时间复杂度为N‘logK。
    • 即，借助堆结构，我们可以在log量级的时间内查找和调整/移动。因此，维护一个K(该题目中是10)大小的小根堆，然后遍历300万的Query，分别和根元素进行对比- 所以，我们最终的时间复杂度是：O(N)+N’*O(logK)，(N为1000万，N’为300万)。
  • 或者：采用trie树，关键字域存该查询串出现的次数，没有出现为0。最后用10个元素的最小推来对出现频率进行排序。

在2.5亿个整数中找出不重复的整数，内存不足以容纳这2.5亿个整数。

  • 方案1：采用2-Bitmap（每个数分配2bit，00表示不存在，01表示出现一次，10表示多次，11无意义）进行，共需内存 内存，还可以接受。然后扫描这2.5亿个整数，查看Bitmap中相对应位，如果是00变01，01变10，10保持不变。所描完事后，查看bitmap，把对应位是01的整数输出即可。
  • 方案2：也可采用上题类似的方法，进行划分小文件的方法。然后在小文件中找出不重复的整数，并排序。然后再进行归并，注意去除重复的元素。

海量数据分布在100台电脑中，想个办法高校统计出这批数据的TOP10。

  • 方案1：
    • 在每台电脑上求出TOP10，可以采用包含10个元素的堆完成（TOP10小，用最大堆，TOP10大，用最小堆）。比如求TOP10大，我们首先取前 10个元素调整成最小堆，如果发现，然后扫描后面的数据，并与堆顶元素比较，如果比堆顶元素大，那么用该元素替换堆顶，然后再调整为最小堆。最后堆中的元 素就是TOP10大。
    • 求出每台电脑上的TOP10后，然后把这100台电脑上的TOP10组合起来，共1000个数据，再利用上面类似的方法求出TOP10就可以了。

怎么在海量数据中找出重复次数最多的一个？

  • 方案1：先做hash，然后求模映射为小文件，求出每个小文件中重复次数最多的一个，并记录重复次数。然后找出上一步求出的数据中重复次数最多的一个就是所求（具体参考前面的题）。

上千万或上亿数据（有重复），统计其中出现次数最多的钱N个数据。

  • 方案1：上千万或上亿的数据，现在的机器的内存应该能存下。所以考虑采用hash_map/搜索二叉树/红黑树等来进行统计次数。然后就是取出前N个出现次数最多的数据了，可以用第6题提到的堆机制完成。

1000万字符串，其中有些是重复的，需要把重复的全部去掉，保留没有重复的字符串。请怎么设计和实现？

  • 方案1：这题用trie树比较合适，hash_map也应该能行。

一个文本文件，大约有一万行，每行一个词，要求统计出其中最频繁出现的前10个词，请给出思想，给出时间复杂度分析。

  • 方案1：这题是考虑时间效率。用trie树统计每个词出现的次数，时间复杂度是O(nle)（le表示单词的平准长度）。然后是找出出现最频繁的 前10个词，可以用堆来实现，前面的题中已经讲到了，时间复杂度是O(nlg10)。所以总的时间复杂度，是O(nle)与O(nlg10)中较大 的哪一个。

一个文本文件，找出前10个经常出现的词，但这次文件比较长，说是上亿行或十亿行，总之无法一次读入内存，问最优解。

  • 方案1：首先根据用hash并求模，将文件分解为多个小文件，对于单个文件利用上题的方法求出每个文件件中10个最常出现的词。然后再进行归并处理，找出最终的10个最常出现的词。

100w个数中找出最大的100个数。

  • 方案1：在前面的题中，我们已经提到了，用一个含100个元素的最小堆完成。复杂度为O(100w*lg100)。
  • 方案2：采用快速排序的思想，每次分割之后只考虑比轴大的一部分，知道比轴大的一部分在比100多的时候，采用传统排序算法排序，取前100个。复杂度为O(100w*100)。
  • 方案3：采用局部淘汰法。选取前100个元素，并排序，记为序列L。然后一次扫描剩余的元素x，与排好序的100个元素中最小的元素比，如果比这个 最小的要大，那么把这个最小的元素删除，并把x利用插入排序的思想，插入到序列L中。依次循环，知道扫描了所有的元素。复杂度为O(100w*100)。

一共有N个机器，每个机器上有N个数。每个机器最多存O(N)个数并对它们操作。如何找到 个数中的中数？

  • 方案1：先大体估计一下这些数的范围，比如这里假设这些数都是32位无符号整数（共有 个）。我们把0到 的整数划分为N个范围段，每个段包含 个整数。比如，第一个段位0到 ，第二段为 到 ，…，第N个段为 到 。 然后，扫描每个机器上的N个数，把属于第一个区段的数放到第一个机器上，属于第二个区段的数放到第二个机器上，…，属于第N个区段的数放到第N个机器上。 注意这个过程每个机器上存储的数应该是O(N)的。下面我们依次统计每个机器上数的个数，一次累加，直到找到第k个机器，在该机器上累加的数大于或等于 ，而在第k-1个机器上的累加数小于 ，并把这个数记为x。那么我们要找的中位数在第k个机器中，排在第 位。然后我们对第k个机器的数排序，并找出第 个数，即为所求的中位数。复杂度是 的。
  • 方案2：先对每台机器上的数进行排序。排好序后，我们采用归并排序的思想，将这N个机器上的数归并起来得到最终的排序。找到第n个便是所求。复杂度是n(i)的。

最大间隙问题

  • 给定n个实数 ，求着n个实数在实轴上向量2个数之间的最大差值，要求线性的时间算法。
  • 方案1：最先想到的方法就是先对这n个数据进行排序，然后一遍扫描即可确定相邻的最大间隙。但该方法不能满足线性时间的要求。故采取如下方法：
    • 找到n个数据中最大和最小数据max和min。
    • 用n-2个点等分区间[min, max]，即将[min, max]等分为n-1个区间（前闭后开区间），将这些区间看作桶，编号为 ，且桶 的上界和桶i+1的下届相同，即每个桶的大小相同。每个桶的大小为： 。实际上，这些桶的边界构成了一个等差数列（首项为min，公差为 ），且认为将min放入第一个桶，将max放入第n-1个桶。
    • 将n个数放入n-1个桶中：将每个元素 分配到某个桶（编号为index），其中 ，并求出分到每个桶的最大最小数据。
    • 最大间隙：除最大最小数据max和min以外的n-2个数据放入n-1个桶中，由抽屉原理可知至少有一个桶是空的，又因为每个桶的大小相同，所以最大间隙 不会在同一桶中出现，一定是某个桶的上界和气候某个桶的下界之间隙，且该量筒之间的桶（即便好在该连个便好之间的桶）一定是空桶。也就是说，最大间隙在桶 i的上界和桶j的下界之间产生 。一遍扫描即可完成。

将多个集合合并成没有交集的集合：给定一个字符串的集合，格式如： 。要求将其中交集不为空的集合合并，要求合并完成的集合之间无交集，例如上例应输出 。

  • (1) 请描述你解决这个问题的思路；
  • (2) 给出主要的处理流程，算法，以及算法的复杂度；
  • (3) 请描述可能的改进。
  • 方案1：采用并查集。首先所有的字符串都在单独的并查集中。然后依扫描每个集合，顺序合并将两个相邻元素合并。例如，对于 ， 首先查看aaa和bbb是否在同一个并查集中，如果不在，那么把它们所在的并查集合并，然后再看bbb和ccc是否在同一个并查集中，如果不在，那么也把 它们所在的并查集合并。接下来再扫描其他的集合，当所有的集合都扫描完了，并查集代表的集合便是所求。复杂度应该是O(NlgN)的。改进的话，首先可以 记录每个节点的根结点，改进查询。合并的时候，可以把大的和小的进行合，这样也减少复杂度。

最大子序列与最大子矩阵问题

  • 数组的最大子序列问题：给定一个数组，其中元素有正，也有负，找出其中一个连续子序列，使和最大。
    • 方案1：这个问题可以动态规划的思想解决。设 表示以第i个元素 结尾的最大子序列，那么显然 。基于这一点可以很快用代码实现。
  • 最大子矩阵问题：给定一个矩阵（二维数组），其中数据有大有小，请找一个子矩阵，使得子矩阵的和最大，并输出这个和。
    • 方案1：可以采用与最大子序列类似的思想来解决。如果我们确定了选择第i列和第j列之间的元素，那么在这个范围内，其实就是一个最大子序列问题。如何确定第i列和第j列可以词用暴搜的方法进行。