CS224WLec6~Lec9-GNN

Background

• DeepWalk/Node2vec属于shallow encoding，有如下优缺点：
  • 需要O(|V|)的参数量，节点间的embedding不共享，每个node有独立的embedding
  • 推导式的（transductive）：training时没有的node，不会有embedding
  • 没有利用到节点的特征，只利用了graph structure
• 范式:
  • encoder生成node embedding，DeepWalk&Node2vec中为一个|V|*D的权重矩阵: $\operatorname{ENC}(v)=\mathbf{z}_{v}$
  • decoder将node embedding映射回原空间，这里存在隐式的decoder，embedding空间两向量的点积可以表示原空间u,v的相似度: $\operatorname{similarity}(u, v) \approx \mathbf{z}_{v}^{\mathrm{T}} \mathbf{z}_{u}$
    • 点积相似度：最小化两向量的模以及夹角余弦的乘积
• GNN: deep encoding
  • encoder为MLP
  • decoder为某种向量相似度

Basics & Intros

Insights

• 其他NN：依赖于IID(independent and identically distributed)，不同样本间是独立的，因此其无需满足排列不变性，而GNN节点间不独立 —》 每个节点的特征依赖于其他节点 —》 节点顺序改变后，输入GNN的特征也会改变 —》 需要满足排列不变性，使得不同的节点排列，也能有同样的结果
• 原则
  • 排列不变性：调整输入节点的顺序，得到的同一个节点的表达应该一致。A为邻接矩阵，X为节点特征矩阵，两种不同的节点顺序下，得到的同一个节点的表达应该一致 $$f\left(\boldsymbol{A}_{1}, \boldsymbol{X}_{1}\right)=f\left(\boldsymbol{A}_{2}, \boldsymbol{X}_{2}\right)$$
• MLP：不满足排列不变性
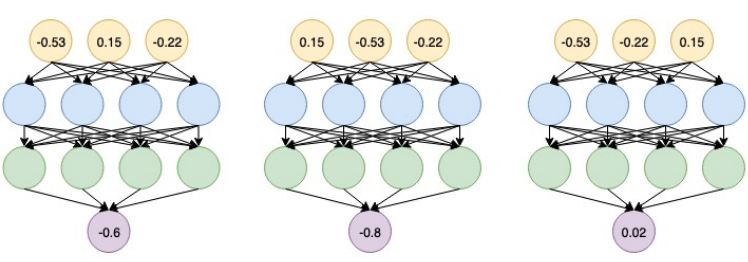
• 利用MLP实现GNN不符合预期
• Insights: 借鉴CNN，每次卷积操作只取某个点及其邻域点
  • 卷积：对邻域信息的提取以及归纳

模型结构

• 利用每个节点的邻域节点为每个节点建立计算图。nn的层数k代表用了k hop的邻域。
• 每个节点都有不同的计算图
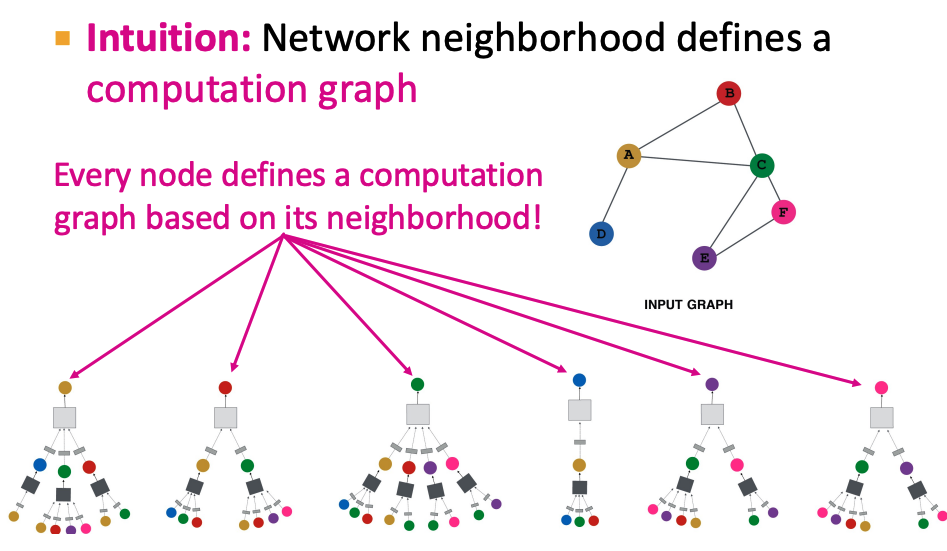
• layer0: node v的输入特征
• layerk: 经过了k跳后，node v的节点信息

模型参数

• 每一层包含两个阶段：信息aggregation & passing
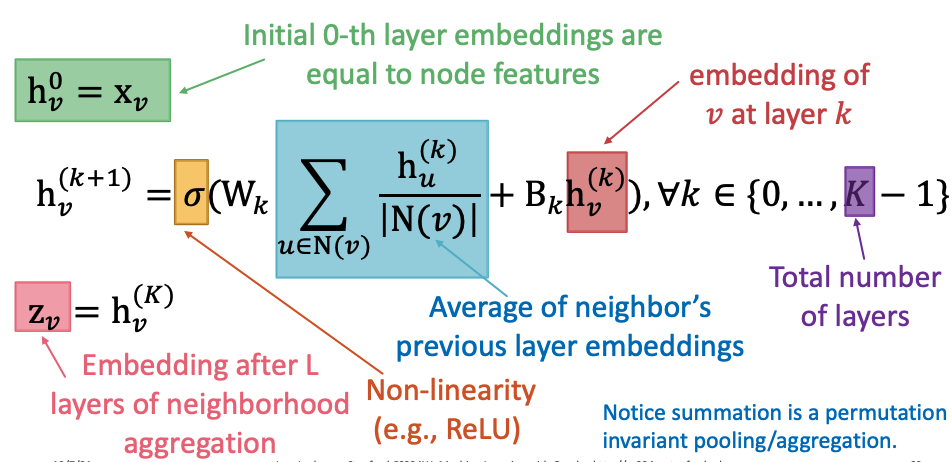
• 每层参数共享
• $h_{v}^{k}$: the hidden representation of node v at layer k
• $W_{k}$: weight matrix for neighborhood aggregation
• $B_{k}$: weight matrix for transforming hidden vector of self
• 当aggregate为简单的平均时，可以转化为稀疏矩阵表达式 —》 稀疏矩阵便于优化

General GNN Framework

A Single GNN Layer

• Goal: Compress a set of vectors into a single vector
• Two steps:
  • Message, v, 传送信息
  • Aggregate
• others:
  • Nonlinearity(activation)：增加表达能力
  • residual/attention/dropout/BatchNorm/…

Message

• 将l-1层的vectors过一个function，得到新的vectors，也称messages。对于每个node u： $$\mathbf{m}_{u}^{(l)}=\mathrm{MSG}^{(l)}\left(\mathbf{h}_{u}^{(l-1)}\right)$$
• 比如使用线性层作为该函数： $$\mathbf{m}_{u}^{(l)}=\mathbf{W}^{(l)} \mathbf{h}_{u}^{(l-1)}$$

Aggregation

• 对于节点v，将其领域内的所有messages聚合在一起 $$\mathbf{h}_{v}^{(l)}=\mathrm{AGG}^{(l)}\left(\left\{\mathbf{m}_{u}^{(l)}, u \in N(v)\right\}\right)$$
• principle: Aggregation需要满足排列不变性

Issues & Solutions

• Issue1: 只考虑了领域，节点本身的信息被丢弃了
• Solution1: 计算${h}_{v}^{(l)}$的时候，考虑 ${h}_{v}^{(l-1)}$，可以认为是node v有一个self-edge
  • Message $$\mathbf{m}_{u}^{(l)}=\mathbf{W}^{(l)} \mathbf{h}_{u}^{(l-1)}, \mathbf{m}_{v}^{(l)}=\mathbf{B}^{(l)} \mathbf{h}_{v}^{(l-1)}$$
  • Aggregation $$\mathbf{m}_{u}^{(l)}=\mathbf{W}^{(l)} \mathbf{h}_{u}^{(l-1)} \mathbf{m}_{v}^{(l)}=\mathbf{B}^{(l)} \mathbf{h}_{v}^{(l-1)}$$
• Issue2:
• Solution2: Residual

Classical GNN Layers

GCN(Graph Convolutional Networks)

• Message：利用出度作归一化。包含了self-edge。
• Aggregation: sum $$\mathbf{h}_{v}^{(l)}=\sigma\left(\sum_{u \in N(v)} \mathbf{W}^{(l)} \frac{\mathbf{h}_{u}^{(l-1)}}{|N(v)|}\right)$$

GraphSAGE

• Message和Aggregation结合在一起，且做了多次Aggregation
• 先对neighbors做aggregate，再和node本身aggregate，之后再计算一次Message
  • 邻域的Aggregation可以是Mean, pool, LSTM等 $$\mathbf{h}_{v}^{(l)}=\sigma\left(\mathbf{w}^{(l)} \cdot \operatorname{CONCAT}\left(\mathbf{h}_{v}^{(l-1)}, \mathrm{AGG}\left(\left\{\mathbf{h}_{u}^{(l-1)}, \forall u \in N(v)\right\}\right)\right)\right)$$
• l2 normalization: Apply l2 normalization to ${h}_{v}^{(l)}$ at every layer。标准化后，每个vector的l2 norm都为1 $$\mathbf{h}_{v}^{(l)} \leftarrow \frac{\mathbf{h}_{v}^{(l)}}{\left\|\mathbf{h}_{v}^{(l)}\right\|_{2}} \forall v \in V$$

GAT

• 显式地获得不同邻域节点对目标节点的重要性
• $$\alpha_{v u} $$ 为u(key)对v(value)的attention. - 例如GCN中 $$ \alpha_{v u}=\frac{1}{|N(v)|} $$ ，每个节点u对v的attention是一样的 $$ \mathbf{h}_{v}^{(l)}=\sigma\left(\sum_{u \in N(v)}{\alpha_{v u}} \mathbf{W}^{(l)} \mathbf{h}_{u}^{(l-1)}\right)$$
• attention计算
  • attention系数计算：相似度/MLP $$e_{v u}=a\left(\mathbf{W}^{(l)} \mathbf{h}_{u}^{(l-1)}, \mathbf{W}^{(l)} \boldsymbol{h}_{v}^{(l-1)}\right)$$
  • 归一化: softmax $$\alpha_{v u}=\frac{\exp \left(e_{v u}\right)}{\sum_{k \in N(v)} \exp \left(e_{v k}\right)}$$
• 多头attention $$\begin{array}{l} \mathbf{h}_{v}^{(l)}[1]=\sigma\left(\sum_{u \in N(v)} \alpha_{v u}^{1} \mathbf{W}^{(l)} \mathbf{h}_{u}^{(l-1)}\right) \\ \mathbf{h}_{v}^{(l)}[2]=\sigma\left(\sum_{u \in N(v)} \alpha_{v u}^{2} \mathbf{W}^{(l)} \mathbf{h}_{u}^{(l-1)}\right) \\ \mathbf{h}_{v}^{(l)}[3]=\sigma\left(\sum_{u \in N(v)} \alpha_{v u}^{3} \mathbf{W}^{(l)} \mathbf{h}_{u}^{(l-1)}\right) \end{array}$$

$$\mathbf{h}_{v}^{(l)}=\mathrm{AGG}\left(\mathbf{h}_{v}^{(l)}[1], \mathbf{h}_{v}^{(l)}[2], \mathbf{h}_{v}^{(l)}[3]\right)$$

• Pros
  • Computationally efficien: attention系数可以并行计算所有的edges；aggregation可以并行计算所有nodes
  • Storage efficient: 不超过O(V+E)

Stacking GNN layers

The over-smoothing problem

• all the node embeddings converge to the same value
• 每个node的embedding由其感受野决定，如果两个node的感受野重合的很多，其embedding越相近。而感受野由GNN的层数决定，层数越多，over-smoothing越严重
• Solution1: GNN层数的控制。先分析感受野大小，再根据所需感受野大小决定layers number
• Solution2: skip connections/residual。
  • 相当于mixture of models. N次skip, $2^{N}$个可能的路径/模型
  • Option1: 连到非线性前 $$\mathbf{h}_{v}^{(l)}=\sigma\left(\sum_{u \in N(v)} \mathbf{W}^{(l)} \frac{\mathbf{h}_{u}^{(l-1)}}{|N(v)|}+\mathbf{h}_{v}^{(l-1)}\right)$$
  • Option2: 连到下一层

提高GNN表达能力

• Solution1: make aggregation / transformation become a deep neural network!
• Solution2: 增加其他层（MLP/CNN等）

Graph Augmentation

• idea: raw input graph ≠ computation graph: 计算图不必和实际的图结构保持一致

Reason for augmentation

• 特征：原始图的特征可能比较少 —》 feature augmentation
• 图结构
  • 图太稀疏：inefficient message passing —》 Add virtual nodes / edges
  • 图太稠密：costly —》 Sample neighbors when doing message passing
  • 图太大：GPU放不下 —》 Sample subgraphs to compute embeddings

Feature augementation

• one-hot/constant encoding
• others: 一般会使用：
  • node degree
  • clustering coefficient
  • pagerank
  • centrality

Sparse graphs augmentation

• add virtual nodes/edges
• Add virtual edges
  • 例如在使用邻接矩阵A的时候，改为使用 $A+A^{2}$，A2相当于添加了virtual edges
• Add vitual nodes
  • 提高稀疏图中的message passing

Node neighborhood sampling

• 针对很稠密的图引起的costly问题
• 方案：sampling
  • 对某个target节点，sample其neighbors
  • sample target节点

GNN training pipeline

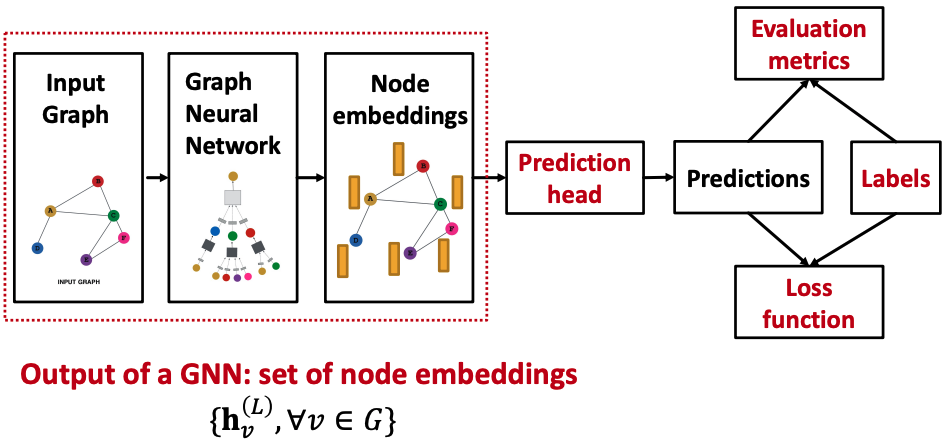
• 以上工作将计算得到set of d-dim node embs
• 还存在两个问题：
  • 这些emb需要被应用在具体的任务中（前向过程需要完善）
  • emb需要更新（反向传播需要定义）

$$\left\{\mathbf{h}_{v}^{(L)} \in \mathbb{R}^{d}, \forall v \in G\right\}$$

Prediction heads

node-level

• 直接利用node embs，其中$\mathbf{W}^{(H)} \in \mathbb{R}^{k * d}$: map node embeddings from $\mathbf{h}_{v}^{(L)} \in \mathbb{R}^{d}$ to $\widehat{\boldsymbol{y}}_{v} \in \mathbb{R}^{k}$ so that we can compute the loss

$$\widehat{\boldsymbol{y}}_{v}=\operatorname{Head}_{\text {node }}\left(\mathbf{h}_{v}^{(L)}\right)=\mathbf{W}^{(H)} \mathbf{h}_{v}^{(L)}$$

edge-level

• 使用pair of node embs
• option1: concat+linear(map 2d-dim to k-dim) $$\left.\widehat{\boldsymbol{y}}_{u v}=\text { Linear(Concat }\left(\mathbf{h}_{u}^{(L)}, \mathbf{h}_{v}^{(L)}\right)\right)$$
• option2: dot product. 得到一个连续值，只能应用于二分类预测/一维回归
• option3: 多头的dot product，多个加权的option2 $$\begin{array}{c} \widehat{\boldsymbol{y}}_{u v}^{(1)}=\left(\mathbf{h}_{u}^{(L)}\right)^{T} \mathbf{W}^{(1)} \mathbf{h}_{v}^{(L)} \\ \widehat{\boldsymbol{y}}_{u v}^{(k)}=\left(\mathbf{h}_{u}^{(L)}\right)^{T} \mathbf{W}^{(k)} \mathbf{h}_{v}^{(L)} \\ \widehat{\boldsymbol{y}}_{u v}=\operatorname{Concat}\left(\widehat{y}_{u v}^{(1)}, \ldots, \widehat{\boldsymbol{y}}_{u v}^{(k)}\right) \in \mathbb{R}^{k} \end{array}$$

graph-level

• option1: global pooling
  • 问题：无法区分不同scale的graph $$\begin{array}{l} \text { Prediction for } G_{1}: \hat{y}_{G}=\operatorname{Sum}(\{-1,-2,0,1,2\})=0 \\ \text { Prediction for } G_{2}: \hat{y}_{G}=\operatorname{Sum}(\{-10,-20,0,10,20\})=0 \end{array}$$
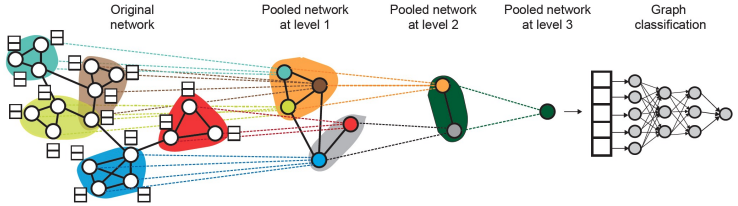
• option2: hierarchically global pooling
  • 需要同时实现两个GNN任务：GNN A：计算node embeddings; GNN B：聚类
  • 两个任务可以并行训练
  • 为每一个cluster创建一个新的node，为相连的nodes创建edge，并生成一个新的pooled network

Loss defines

• 和其他nn无区别

Dataset split

• 难点：graph的各个node/edge之间不满足iid假设。random split会带来information leakage。
• solution1(Transductive setting): 会有部分leakage。仅仅split node labels.
  • At training time, we compute embeddings using the entire graph, and train using node 1&2’s labels
  • At validation time, we compute embeddings using the entire graph, and evaluate on node 3&4’s labels
  • training / validation / test sets都在同一个graph上。三个dataset组成一个graph。
  • 可以应用在node/edge tasks。因为graph task需要在unseen graphs上做测试，而transductive方法无法满足。
• solution2(Inductive setting): We break the edges between splits to get multiple graphs。没有信息泄漏，图被分成了三个子图。
  • At training time, we compute embeddings using the graph over node 1&2, and train using node 1&2’s labels
  • At validation time, we compute embeddings using the graph over node 3&4, and evaluate on node 3&4’s labels
  • training / validation / test sets不在同一个graph上。三个dataset组成是三个graph。
  • 可以应用在node/edge/graph tasks

link prediction

• link prediction是无监督任务，需要定义label & split
• step1: 先划分message edges和supervision edges。其中supervision edges不入图，只作为label。
• step2: split
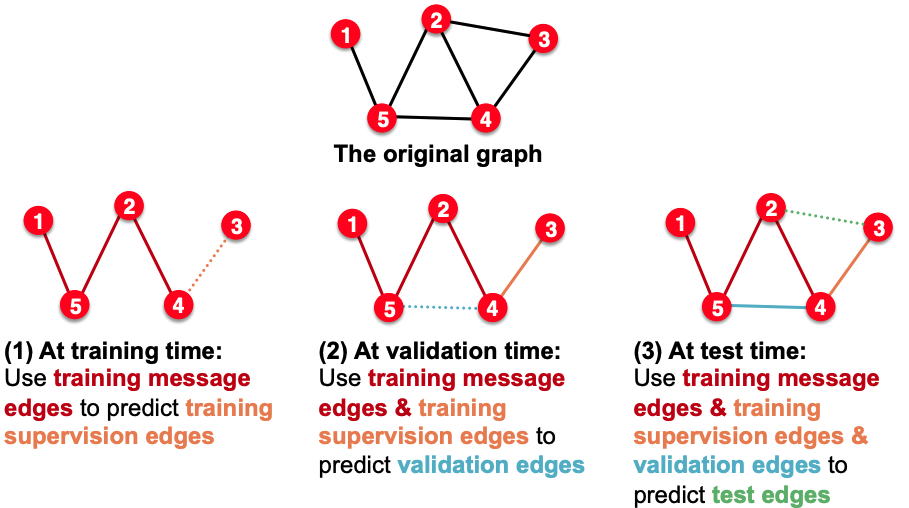
  • Transductive method: 有四种edge: training message edges & training supervision edges & validation edges & predict test edges.
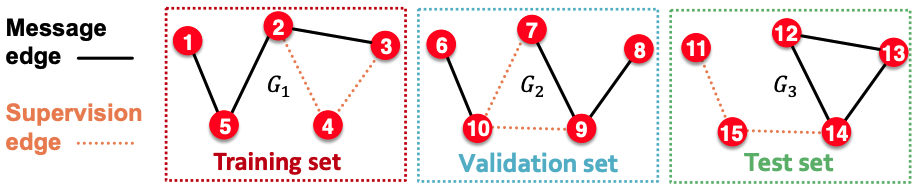
  • Inductive method: In train or val or test set, each graph will have 2 types of edges。

Tips

• data processing: use normalization
• optimizer: adam is relatively robust to learning rate
• activation: relu
• bias term in every layer
• debug:
  • 小数据集上，loss应该很小。如果underfit, something is wrong
  • loss
  • visualizations
  • initialization
  • adjust hyperparameters such as learning rate

性质

• 本质：假设将节点作为特征向量作为输入feed into MLP, 特征向量会包含邻域节点的信息，因此不能满足排列不变性，而GNN则是把节点的领域信息存在了NN结构里，因此每个节点都拥有自己的计算图/神经网络结构
• 流程：1）定义neighborhood aggregation function; 2) 定义loss function; 3) train; 4) generate node embeddings
• 权重矩阵共享：参数量为|V|的次线性
• Inductive(归纳式的)：可以为没出现过的node生成embedding。由于权重矩阵W/B的共享，即使没有出现过的node，也可以为其生成计算图，进而生成embedding
• 可以为新的graph生成embedding，前提是new graph中的节点都出现在了old graph中

与MLP/CNN/Transformer的异同

GNN VS MLP

• MLP假设IID，不同样本间独立，因此无需满足排列不变性
• Graph数据node间不独立，因此需要满足排列不变性
• 将node的特征向量作为输入，使用MLP —》 将graph的结构作为MLP的输入 —》 一般一个数据集就一种nn结构
• GNN —》 将graph的结构作为nn的结构 —》 一个graph有多种nn结构

GNN VS CNN

• GNN: $\mathrm{h}_{v}^{(l+1)}=\sigma\left(\mathrm{W}_{l} \sum_{u \in \mathrm{N}(v)} \frac{\mathrm{h}_{u}^{(l)}}{|\mathrm{N}(v)|}+\mathrm{B}_{l} \mathrm{~h}_{v}^{(l)}\right), \forall l \in\{0, \ldots, L-1\}$
• CNN: $\mathrm{h}_{v}^{(l+1)}=\sigma\left(\sum_{u \in \mathrm{N}(v) \cup\{v\}} \mathrm{W}_{l}^{u} \mathrm{~h}_{u}^{(l)}\right), \forall l \in\{0, \ldots, L-1\}$
• 重写CNN：$\mathrm{h}_{v}^{(l+1)}=\sigma\left(\sum_{u \in \mathrm{N}(v)} \mathrm{W}_{l}^{u} \mathrm{~h}_{u}^{(l)}+\mathrm{B}_{l} \mathrm{~h}_{v}^{(l)}\right), \forall l \in\{0, \ldots, L-1\}$
• 从邻域选择讲，CNN是邻域确定的特殊GNN
• CNN不满足排列不变性，改变像素排列，输出也不同

GNN VS Transformer

• Transformer是针对序列数据的，一个序列中两个node互为上下文，因此可以看做是所有n ode都互相连接的graph

GNN Theory

• GNN表达能力的衡量，如何设计表达能力强的GNN
• 表达能力强的GNN能够为不同的节点生成不同的embedding

GNN的表达能力

• GNN的计算图：每个节点的有根子树
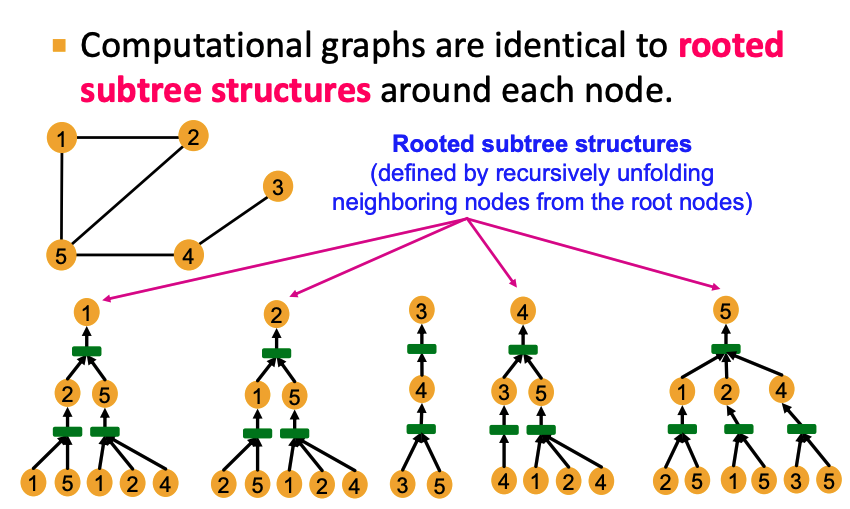
• Injective function: 内射函数。f(x)=Y，不同的X能映射为不同的Y，称之为内射函数
• 如果每一步的neighbor aggregation是内射函数，则GNN可以分辨不同的有根子树。
• GCN(mean-pool, ex. MeanPool([1,0],[0,1])与MeanPool([1,0],[0,1],[1,0],[0,1])一样)/GraphSAGE(max-pool)都不是内射函数
• Any injective multi-set function can be expressed as: $\Phi\left(\sum_{x \in S} f(x)\right)$, f和外层φ为非线性函数，中间是对multi-set做sum。而非线性函数可以用MLP来建模

GIN(Graph Isomorphism Network)

• THE most expressive GNN in the class of message-passing GNNs
• Apply an MLP, element-wise sum, followed by another MLP. $$\mathrm{MLP}_{\Phi}\left(\sum_{x \in S} \operatorname{MLP}_{f}(x)\right)$$

Refs

• ppt Lec6: Graph Neural Networks 1: GNN Model
• ppt Lec7: Graph Neural Networks 2: Design Space
• ppt Lec8: Applications of Graph Neural Networks
• ppt Lec9: Theory of Graph Neural Networks