CS224WLec3-Node Embeddings

Basic

• goal: 为node生成一个embedding
• 两个要素：encoder/相似度计量方法（encode前后都需要）
• framework: encoder 生成embedding —> 相似度计量方法决定embedding学习的好坏
• unsupervised/self-supervised way based on random walks
• task independent

Method

• goal: 原始graph中相似的node获得的embeddings也是相似的
• 类似于word2vec: 目标是求node u的embedding $\mathbf{z}_{u}$,而模型的预测目标是：$P\left(v \mid \mathbf{z}_{u}\right)$，即node v出现在以node u开始的walk上的概率。
• 如何获得“句子”：random walk
• 范式:
  • encoder生成node embedding，本节的encoder为word2vec中的权重矩阵: $\operatorname{ENC}(v)=\mathbf{z}_{v}$
  • decoder将node embedding映射回原空间，这里存在隐式的decoder，embedding空间两向量的点积可以表示原空间u,v的相似度: $\operatorname{similarity}(u, v) \approx \mathbf{z}_{v}^{\mathrm{T}} \mathbf{z}_{u}$
    • 点击相似度：最小化两向量的模以及夹角余弦的乘积

Deep Walk

Random Walk

• 出发点：如果一个random walk中包括从u到v的路径，那u和v是相似的/有相似的高维的多跳信息
• 本质：DFS
• $ N_{\mathrm{R}}(u) $为策略R下，从u出发的walk中，出现的所有nodes $$\max _{f} \sum_{u \in V} \log \mathrm{P}\left(N_{\mathrm{R}}(u) \mid \mathbf{z}_{u}\right)$$ —》 $$\mathcal{L}=\sum_{u \in V} \sum_{v \in N_{R}(u)}-\log \left(P\left(v \mid \mathbf{z}_{u}\right)\right)$$
• 利用softmax求p $$P\left(v \mid \mathbf{z}_{u}\right)=\frac{\exp \left(\mathbf{z}_{u}^{\mathrm{T}} \mathbf{z}_{v}\right)}{\sum_{n \in V} \exp \left(\mathbf{z}_{u}^{\mathrm{T}} \mathbf{z}_{n}\right)}$$
• problem: softmax分母 以及 最外层都需要|V|次遍历 —》$\mathrm{O}\left(|\mathrm{V}|^{2}\right)$的复杂度 —》优化

Negative Sampling

• 使用所有样本做normalization —> 只采样k个负样本做normalization $$P\left(v \mid \mathbf{z}_{u}\right)=\frac{\exp \left(\mathbf{z}_{u}^{\mathrm{T}} \mathbf{z}_{v}\right)}{\sum_{n \in V } \exp \left(\mathbf{z}_{u}^{\mathrm{T}} \mathbf{z}_{n}\right)} \approx \log \left(\sigma\left(\mathbf{z}_{u}^{\mathrm{T}} \mathbf{z}_{v}\right)\right)-\sum_{i=1}^{k} \log \left(\sigma\left(\mathbf{z}_{u}^{\mathrm{T}} \mathbf{z}_{n_{i}}\right)\right), n_{i} \sim P_{V}$$
• k的选择：
  • k越大，模型越鲁棒
  • k越大，对负样本考虑的越多
  • 5~20间较常见
• 负样本的选择：可以选择graph内任意样本，但更准确的方法是选择不在walk中的样本

Node2vec: better random walk strategy

• 简单的random walk会限制walk中的node相似度与graph中node相似度的一致性

Biased 2nd-order random Walks

• trade off between local and global views of the network: BFS & DFS
• 当前在w, 上一步在s的walk，有三种行走方向
  • 退后：回退到s
  • 保持：走到和s距离一致的一个节点
  • 前进：走到距离s更远的节点
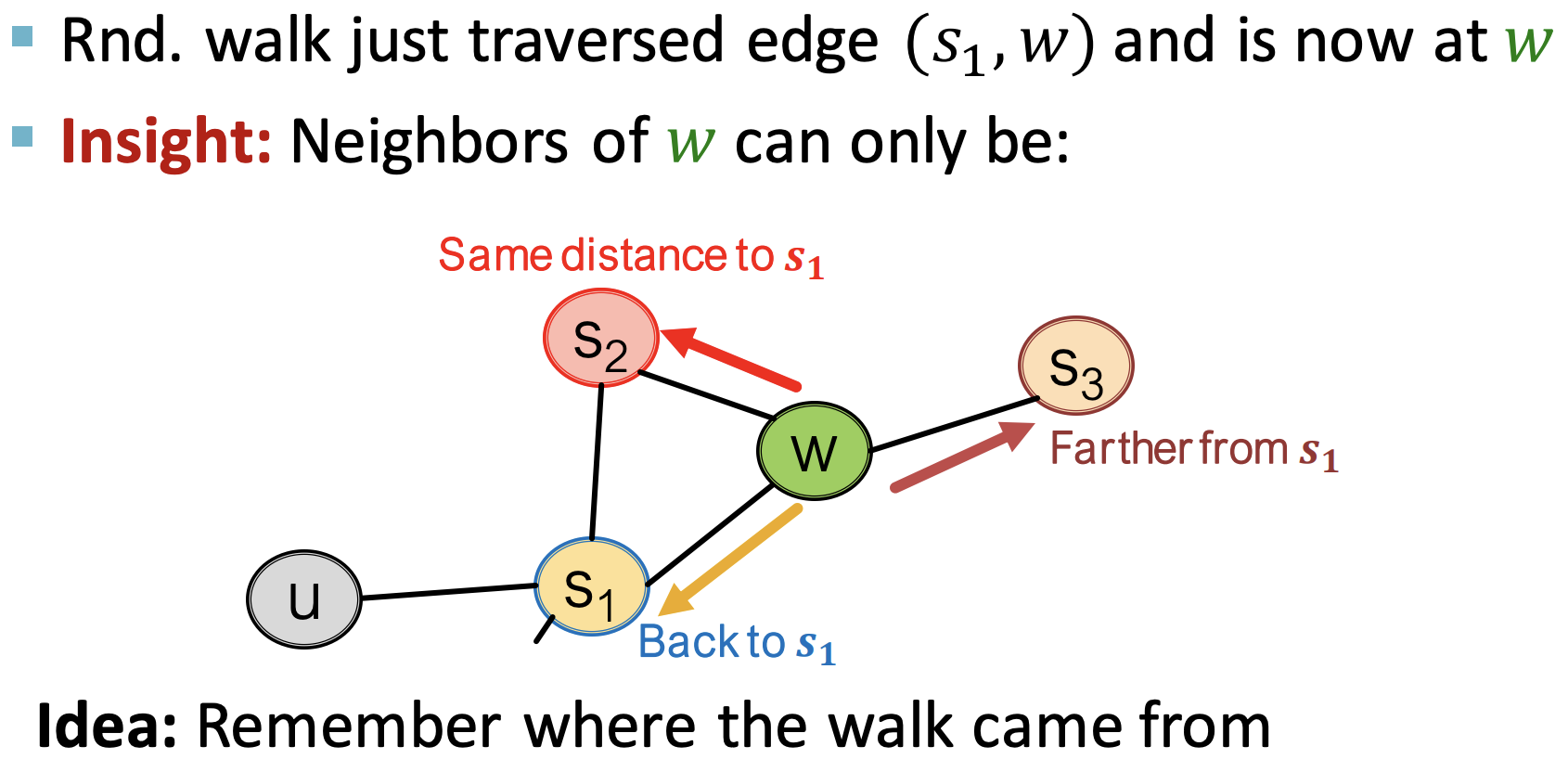
• 实现：两个超参p/q，以及“1”来以非归一化的方法表示上述三种情况的概率
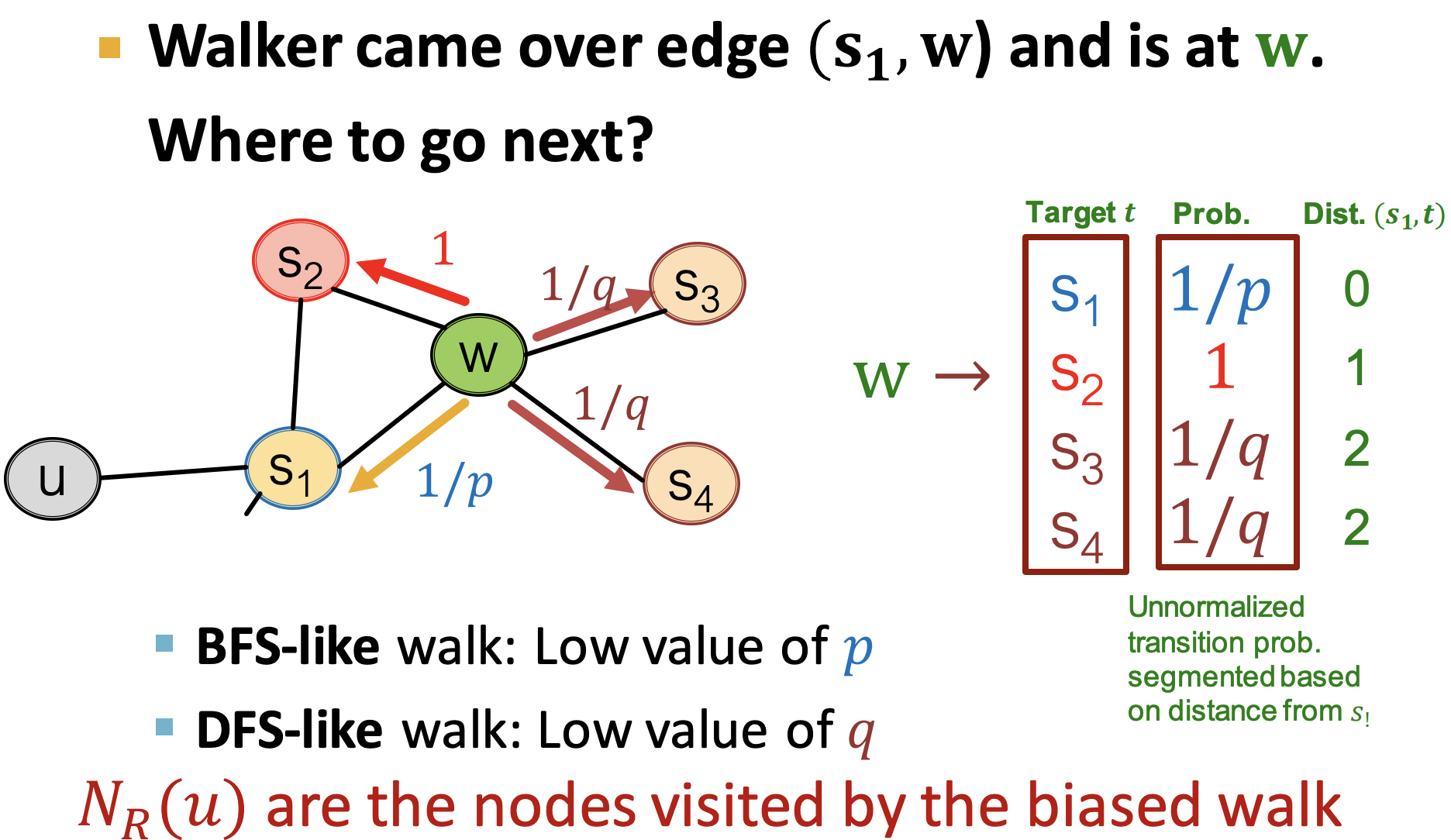
• 流程
  • Compute random walk probabilities
  • Simulate 𝑟 random walks of length 𝑙 starting from each node 𝑢
  • Optimize the node2vec objective using Stochastic Gradient Descent
• Linear-time complexity
• All 3 steps are individually parallelizable

Embedding entire graphs

• approach1: add all node embeddings
• approach2: introduce a “virtual node” or “super node” to represent the graph and learning embedding for this graph
• approach3: anonymous walks embeddings

Anonymous walk embeddings

• Anonymous walk: random walk —> 将node表示为距离start node的去重index。因此，确定了walk length的时候，就确定了anonymous walk中index的个数。
• 方法1：长度为l的annoy walk共有n种情况 —> 做m次random walks —> 统计每种情况的count，并形成一个vector
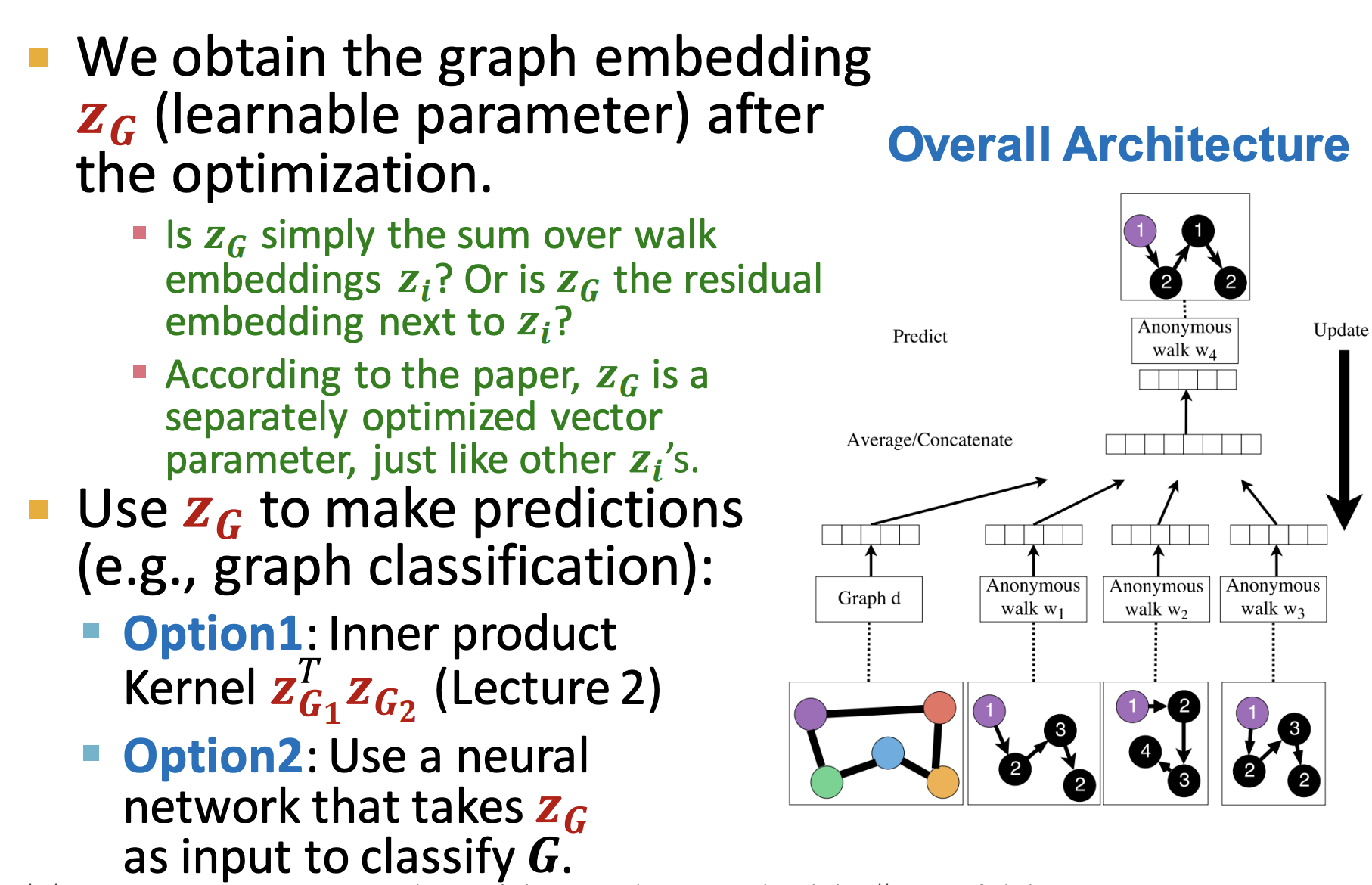
• 方法2：用Anonymous walks的概率分布，学习图的embedding
  • Learn to predict walks that co-occur in 𝚫-size window (e.g., predict 𝑤3 given 𝑤1, 𝑤2 if Δ = 2)
  • objective: $$\max _{z_{G}} \sum_{t=\Delta+1}^{T} \log P\left(w_{t} \mid w_{t-\Delta}, \ldots, w_{t-1}, \mathbf{z}_{G}\right)$$

Pros & Cons

• 属于shallow encoding，有如下优缺点：
  • 需要O(|V|)的参数量，节点间的embedding不共享，每个node有独立的embedding
  • training时没有的node，不会有embedding
  • 没有利用到节点的特征，只利用了graph structure

Reference

• ppt