机器学习中的Metrics&Losses

Posted on Edited on In

机器学习中的Metrics&Losses

分类

交叉熵 & Logloss & Softmax loss

Logloss

Softmax Loss

  • softmax loss为采用softmax(logit)的交叉熵
  • 指数函数可能会有溢出问题，因此可以作数值优化：
    1
    2
    3
    def stable_softmax(X):
        exps = np.exp(X - np.max(X))
        return exps / np.sum(exps)
  • 推导：
  • 导数求解：https://deepnotes.io/softmax-crossentropy
  • 性质
    • 参数冗余（overparameterized​）：所有参数减去一个值，loss相同—》对任何一个拟合数据的假设而言，多种参数取值有可能得到同样的假设。处理方法：1）加正则；2）只优化k-1个类别的参数，比如二分类的logloss。softmax回归原理与实现

ACC(Accuracy)

  • Accuracy = 预测正确的样本数量 / 总样本数量 = (TP+TN) / (TP+FP+TN+FN)

Precision查准

  • Precision = TP / (TP+FP)

Recall/TPR查全

  • Recall = TPR = TP / (TP+FN)

F1&Fn

F1

  • precision和recall的调和平均

Fn

  • 可用来解决分类不均衡问题/对precision和recall进行强调
    • 如F1认为precision和recall同等重要，F2认为recall的重要程度是precision的2倍

P-R曲线(Precision-Recall)

  • P为纵轴，R为横轴
  • 主要关心正例
  • 公式：

FPR

  • FPR = FP/(FP+TN) 真实label为0的样本中，被预测为1的样本占的比例

ROC曲线&AUC

  • 衡量分类准确性，同时考虑了模型对正样本(TPR)和负样本(FPR)的分类能力，因此在样本非均衡的情况下也能做出合理的评价。侧重于排序。

ROC(Receiver operating characteristic curve)

  • 横轴FPR，纵轴TPR
  • ROC曲线在绘制时，需要先对所有样本的预测概率做排序，并不断取不同的阈值计算TPR和FPR，因此AUC在计算时会侧重于排序。

AUC(Area under Curve)

  • ROC曲线与x轴的面积
  • 一般认为：AUC最小值=0.5（其实存在AUC小于0.5的情况，例如每次都预测与真实值相反的情况，但是这种情况，只要把预测值取反就可以得到大于0.5的值，因此还是认为AUC最小值=0.5）
  • AUC的物理意义为任取一对正例和负例，正例得分大于负例得分的概率，AUC越大，表明方法效果越好。—> 排序

    分母是正负样本总的组合数，分子是正样本大于负样本的组合数

  • 计算方式1：n个样本，按照预估值倒序，每个样本rank值赋n…1，计算所有正例的rank值之和，减去排在每个正例后面的正例个数
  • 计算方式2：减去排错的样本对，排错的样本对：对每个正样本，累积排在前面的负样本，再求和。
    • n个样本，按照预估值倒序，neg_counter = 0, rate_counter = 0
    • 遍历：对负例，neg_counter += 1；对正例，rate_counter += neg_counter
    • 结果：

回归

MSE

  • MSE可以理解为，假设整体分布与样本分布误差满足下的最大似然估计，见：https://chenzk1.github.io/2022/04/23/MLE-MAP/#Case2-MSE-Loss 。这里先验假设可以理解为：
    • 1）MSE对误差的假设先验分布为: 0均值常数方差N(0, σ^2)的单峰高斯分布
    • 2）MSE对样本的假设先验分布为: 对于某个样本i，其出现的概率为整体分布在该样本上的值为均值，方差为0，即N(y’_i, σ^2)的单峰高斯分布
    • 3）以上两种假设等价
  • 问题
    • 1）基于单峰高斯分布，建模多峰分布比较困难；
    • 2）相当于MAE的二次函数，大于1的时候loss值较大，对异常值很敏感，很容易造成梯度爆炸打偏模型。在实际使用中稳定性很差。

Hubor Loss

  • 缓解MSE对异常值敏感的问题：超参δ ~ 0时，huber loss趋于MAE，反之趋于MSE；在label异常大时，转为绝对值较小的MAE，反之用MSE保证训练强度。
  • 缺点：单峰高斯分布假设问题同样没有改善。

回归转分类

  • 回归的问题：受样本分布影响较大，对异常值敏感，容易出现梯度计算不稳定、样本分布不满足先验假设的情况。
    • case1: MSE建立在误差满足单峰高斯分布的先验假设下，不满足该假设则
    • case2: 回归问题对异常值敏感，例如label的分布上下界较大，使用MSE时label越大loss越大，容易使模型被label大的样本dominate
  • 回归比分类更难吗？

Softmax

  • 分桶离散化，将回归转化为学习离散后多分类的问题。例如k个分桶时：
  • 优势：避开样本先验分布的假设，可以拟合任意分布
  • 不足：对分桶敏感，分桶策略决定模型学习难度以及预估效果

Distill Softmax

  • 借鉴蒸馏的思想，有分类的优势，也保留了回归的特性（label连续）
  • 分k个桶，tk为桶边界或桶的中心点，f(tk, y)为用于软化概率分布的函数，只与tk，y有关，例如|tk-y|的函数，pk为模型预测在桶k内的概率
  • 例如使用exp^2函数的loss:

Weighted cross entropy

  • 原始Weighted cross entropy

    • Weighted cross entropy本身由youtube提出，用来把时长融入ctr模型中，参考paper。做法为：把正例的label由1改为时长t，负例label仍为0
    • k表示正例数量，P(y)为预估ctr，E(t)为预估时长的数学期望，即样本i的预估时长为：。因为忽略了P(y)，所以是有偏估计。
    • 无偏性修正：分母本来是n-k代表负例数量，改为n之后有偏 -》即负例数量多了k个，为了纠偏需要加入额外的k个正例。

  • 无偏WCE

    • 把回归中每个label=y的样本当做二分类的y个正样本和1个负样本，设预估正样本的概率为pred/(1+pred)，然后用交叉熵计算loss（只适用于y非负的情况）
    • P.S. 转为二分类时，当做y个正样本和1个负样本是无偏的，单纯把y转为y/(y+1)做交叉熵是有偏的。

    | | 回归 | WCE分类 |
    | :———————-: | :———————-: | :————: |
    | 真实值 | 样本i，labeli=ki | ki个正样本，1个负样本 |
    | 预估值 | 样本i，模型预测值yi=predi | 模型预测值仍然是yi=predi，p+（类似pctr）, p+=pred/(1+pred) |
    | 无偏性 | 原分布，预测值的均值为∑y/N | 需要证明预测值的期望为原分布的均值。，则E[pred]=∑y/N，即无偏 |

    • loss：
    • 用表示loss：
    • 样本分布的假设：当时, 令 ，则，即假设样本满足几何分布，几何分布的数学期望为，即WCE的预估值等于几何分布的数学期望，是无偏的。
    • 问题：低估和高估的时候梯度不对称，低估梯度大而高估梯度小，因此实践中使用WCE容易发生高估。将label变换到1附近的区间，可以减少高低估时的梯度差异。

区分度

KS(Kolmogorov-Smirnov)

  • KS用于模型风险区分能力进行评估，指标衡量的是好坏样本累计分布之间的差值。好坏样本累计差异越大，KS指标越大，那么模型的风险区分能力越强。
  • KS的计算步骤如下：
    • 1)计算每个评分区间的好坏账户数。
    • 2)计算每个评分区间的累计好账户数占总好账户数比率(good%)和累计坏账户数占总坏账户数比率(bad%)。
    • 3)计算每个评分区间累计坏账户占比与累计好账户占比差的绝对值（累计good%-累计bad%），然后对这些绝对值取最大值即得此评分卡的K-S值。
  • 低分段累计坏百分比应高于累计好百分比，之后会经历两者差距先扩大再缩小的变化
    KS-曲线

gini

  • 计算每个评分区间的好坏账户数。
  • 计算每个评分区间的累计好账户数占总好账户数比率（累计good%）和累计坏账户数占总坏账户数比率(累计bad%)。
  • 按照累计好账户占比和累计坏账户占比得出下图所示曲线ADC。
  • 计算出图中阴影部分面积，阴影面积占直角三角形ABC面积的百分比，即为GINI系数。

排序

  • http://note.youdao.com/s/D64Y5VaG
  • map和ndcg都是属于per item的评估，即逐条对搜索结果进行分等级的打分，并计算其指标。
  • 基于precision的指标，例如MAP，每个条目的值是的评价用0或1表示；而DCG可以使用多值指标来评价。
  • 基于precision的指标，天然考虑了排序信息。

map@k

prec@k

  • k指到第k个正确的召回结果，precision的值
    • 这里$\pi$代表documents list，即推送结果列。$I$是指示函数，$\pi^{(-1)}(t)$代表排在位置$t$处的document的标签（相关为1，否则为0）。这一项可以理解为前k个documents中，标签为1的documents个数与k的比值。
  • 只能表示单点的策略效果

ap@k

  • 其中$m_1$代表与该query相关的document的数量（即真实标签为1），$m$则代表模型找出的前$m$个documents，本例中 [公式] ，并假设 [公式] ，即真正和query相关的document有6个。（但是被模型找出来的7个doc中仅仅有3个标签为1，说明这个模型召回并不怎么样）
  • @1到@k的precision的平均

map@k

  • 多个query的ap@k平均

ndcg

  • 基于CG的评价指标允许我们使用多值评价一个item：例如对一个结果可评价为Good（好）、Fair（一般）、Bad（差），然后可以赋予为3、2、1.

cg(Cumulative Gain)

  • CG是在这个查询输出结果里面所有的结果的等级对应的得分的总和。如一个输出结果页面有P个结果.

dcg(Discounted Cumulative Gain)

  • 取对数是因为：根据大量的用户点击与其所点内容的位置信息，模拟出一条衰减的曲线。

ndcg(normalize DCG)

  • IDCG（Ideal DCG）就是理想的DCG。
  • IDCG如何计算？首先要拿到搜索的结果，然后对这些结果进行排序，排到最好的状态后，算出这个排列下的DCG，就是iDCG。因此nDCG是一个0-1的值，nDCG越靠近1，说明策略效果越好，或者说只要nDCG<1，策略就存在优化调整空间。因为nDCG是一个相对比值，那么不同的搜索结果之间就可以通过比较nDCG来决定哪个排序比较好。

MRR(Mean Reciprocal Rank)

  • 其中|Q|是查询个数，$rank_i$是第i个查询，第一个相关的结果所在的排列位置

检测

  • 评价一个检测算法时，主要看两个指标
    • 是否正确的预测了框内物体的类别
    • 预测的框和人工标注框的重合程度

mAP

  • 求取每个类别的ap的平均值
    • 即，对每个类别进行预测，得到其预测值的排序，求ap
    • 求map

IOU(Interest Over Union)

检测里的IOU

  • 框的IOU示意

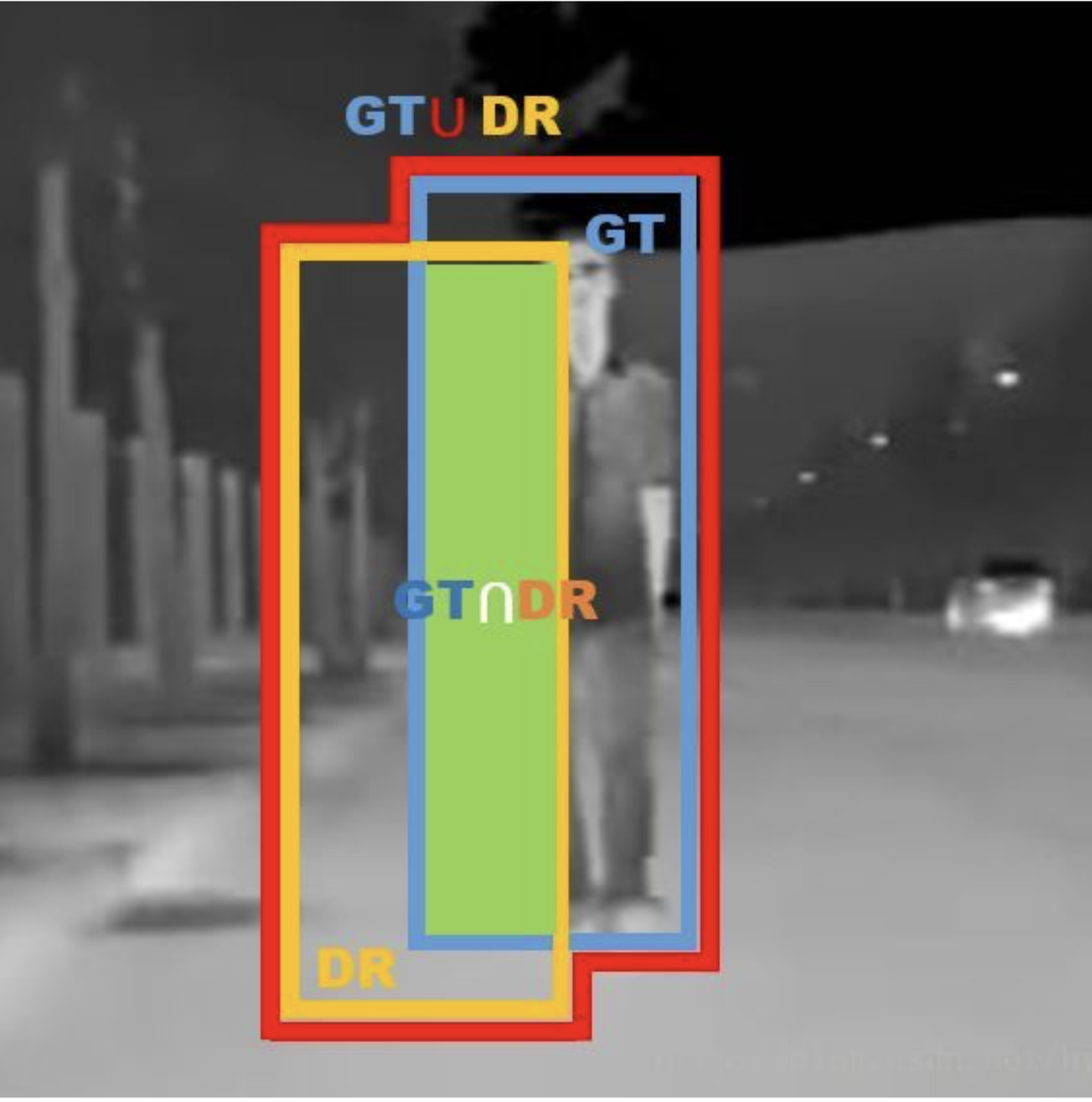
语义分割里的IOU

  • 像素集合的IOU
  • $p{ij}$表示真实值为i，被预测为j的数量， K+1是类别个数（包含空类）。$p{ii}$是真正的数量。$p{ij}$、$p{ji}$则分别表示假正和假负。

mIOU(mean IOU)

  • blog
  • 用于语义分割