ML-Decision Tree

Posted on Edited on In

[TOC]

  1. 决策树

问题：如何挑选用于分裂节点的特征—>ID3 C4.5 …(一个标准：使分裂出来的节点尽可能纯，即一个分支尽可能属于同类)

  1. ID3
    信息增益

    信息增益 = 信息熵 - 条件熵

    • 信息增益：针对每个 属性
    • 信息熵：整个样本空间的不确定度。其中Pk一定是label取值的概率。

    • 条件熵：给定某个属性，求其信息熵

      —> 问题：某属性所包括的类别越多，信息增益越大。极限：每个类别仅有1个实例（label数量为1），log p = log1 = 0， 所以最终条件熵=0。或：属性类别越多，条件熵越小，其纯度越高。

      —> 信息增益准则其实是对可取值数目较多的属性有所偏好！

      —> 泛化能力不强

  2. C4.5 信息增益率+信息增益

    属性a的信息增益率 = 属性a的信息增益 / a的某个固有统计量IV(a)

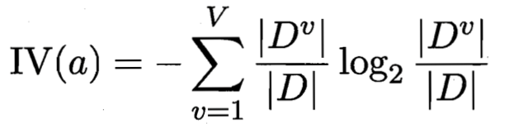
    IV(a)公式

    V为a的取值数目。
    （实际上是属性a的信息熵）

    • 直接使用信息增益率：偏好取值数目小的属性。
    • 先选择高于平均水平信息增益的属性，再选择最高信息增益率的属性。

  3. CART 基尼系数+MAE/MSE

    与ID3、C4.5的不同：形成二叉树，因此 —> 既要确定要分割的属性，也要确定要分割的值

    • 回归树：MAE/MSE

      • example(MSE)：
        1. 考虑数据集 D 上的所有特征 j，遍历每一个特征下所有可能的取值或者切分点 s，将数据集 D 划分成两部分 D1 和 D2
        2. 分别计算上述两个子集的平方误差和，选择最小的平方误差对应的特征与分割点，生成两个子节点。
        3. 对上述两个子节点递归调用步骤1 2,直到满足停止条件。

    • 分类树：(Gini不纯度)

      某属性A的基尼不纯度
      基尼不纯度越小，纯度越高

    1. 对每个特征 A，对它的所有可能取值 a，将数据集分为 A＝a，和 A!＝a 两个子集，计算集合 D 的基尼指数：
      Gini(A) = D1/D Gini(D1) + D2/D Gini(D2)
    2. 遍历所有的特征 A，计算其所有可能取值 a 的基尼指数，选择 D 的基尼指数最小值对应的特征及切分点作为最优的划分，将数据分为两个子集。
    3. 对上述两个子节点递归调用步骤1 2, 直到满足停止条件。
    4. 生成 CART 决策树。
    停止条件有：
1. 节点中的样本个数小于预定阈值;
2. 样本集的Gini系数小于预定阈值（此时样本基本属于同一类）;
3. 没有更多特征。

  4. 控制决策树过拟合的方法

    • 剪枝
    • 控制终止条件，避免树形结构过细
    • 构建随机森林