ML-DBSCAN以及sklearn实现DBSCAN
[TOC]
原文1
原文2
DBSCAN(Density-Based Spatial Clustering of Applications with Noise,具有噪声的基于密度的聚类方法)是一种很典型的密度聚类算法,和K-Means,BIRCH这些一般只适用于凸样本集的聚类相比,DBSCAN既可以适用于凸样本集,也可以适用于非凸样本集。
密度聚类
其原理为:同一类别的样本,其样本分布一定是紧密的;可以将各组紧密相连的样本划分为不同的类别来得到聚类类别结果。
DBSCAN
关键概念
参数(ϵ, MinPts)描述领域的样本分布紧密程度,其中ϵ描述了某一样本的领域距离阈值,MinPts描述某一样本的距离为ϵ的领域中样本个数的阈值。
假设样本集是D=(x1,x2,…,xm),则DBSCAN具体的密度描述定义如下:
- ϵ-邻域:对于xj∈D,其ϵ-邻域包含样本集D中与xj的距离不大于ϵ的子样本集,即Nϵ(xj)={xi∈D|distance(xi,xj)≤ϵ}, 这个子样本集的个数记为|Nϵ(xj)|
- 核心对象:对于任一样本xj∈D,如果其ϵ-邻域对应的Nϵ(xj)至少包含MinPts个样本,即如果|Nϵ(xj)|≥MinPts,则xj是核心对象。
- 密度直达:如果xi位于xj的ϵ-邻域中,且xj是核心对象,则称xi由xj密度直达。
- 密度可达:对于xi和xj,如果存在样本样本序列p1,p2,…,pT,满足p1=xi,pT=xj, 且pt+1由pt密度直达,则称xj由xi密度可达。也就是说,密度可达满足传递性。此时序列中的传递样本p1,p2,…,pT−1均为核心对象,因为只有核心对象才能使其他样本密度直达。
- 密度相连:对于xi和xj,如果存在核心对象样本xk,使xi和xj均由xk密度可达,则称xi和xj密度相连。注意密度相连关系是满足对称性的。
图中MinPts = 5。红点为核心对象。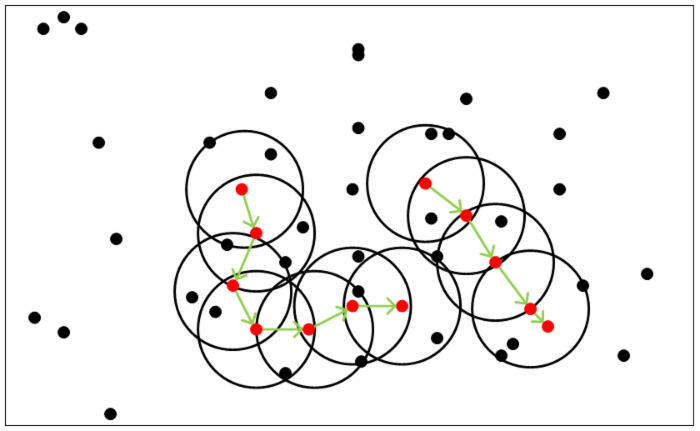
聚类思想
由密度可达关系导出的最大密度相连的样本集合,即为最终聚类的一个类别。
方法:任意选择一个没有类别的核心对象作为种子,然后找到该核心对象密度可达的样本集合,为一个聚类。接着选择另一个没有类比的核心对象…直到所有核心对象都有类别。
问题:
- outlier.不在任何一个核心对象周围的点定义为异常样本点或噪声点,不考虑。
- 距离。少量样本而言,搜索周围样本一般用最近邻的方法;大量样本,可以用KD树,球树等搜索最近邻。
- 若某样本到两个核心对象的距离都小于ϵ,但这两个核心对象不可达,此时采取先来后到原则,标记其为先聚类的cluster类别。
算法
输入:样本集D=(x1,x2,…,xm),邻域参数(ϵ,MinPts), 样本距离度量方式
输出: 簇划分C.
- 初始化核心对象集合Ω=∅, 初始化聚类簇数k=0,初始化未访问样本集合Γ = D, 簇划分C = ∅
- 对于j=1,2,…m, 按下面的步骤找出所有的核心对象:
- 通过距离度量方式,找到样本xj的ϵ-邻域子样本集Nϵ(xj)
- 如果子样本集样本个数满足|Nϵ(xj)|≥MinPts, 将样本xj加入核心对象样本集合:Ω=Ω∪{xj}
- 如果核心对象集合Ω=∅,则算法结束,否则转入步骤4.
- 在核心对象集合Ω中,随机选择一个核心对象o,初始化当前簇核心对象队列Ωcur={o}, 初始化类别序号k=k+1,初始化当前簇样本集合Ck={o}, 更新未访问样本集合Γ=Γ−{o}
- 如果当前簇核心对象队列Ωcur=∅,则当前聚类簇Ck生成完毕, 更新簇划分C={C1,C2,…,Ck}, 更新核心对象集合Ω=Ω−Ck, 转入步骤3。
- 在当前簇核心对象队列Ωcur中取出一个核心对象o′,通过邻域距离阈值ϵ找出所有的ϵ-邻域子样本集Nϵ(o′),令Δ=Nϵ(o′)∩Γ, 更新当前簇样本集合Ck=Ck∪Δ, 更新未访问样本集合Γ=Γ−Δ, 更新Ωcur=Ωcur∪(Δ∩Ω)−o′,转入步骤5.
输出结果为: 簇划分C={C1,C2,…,Ck}
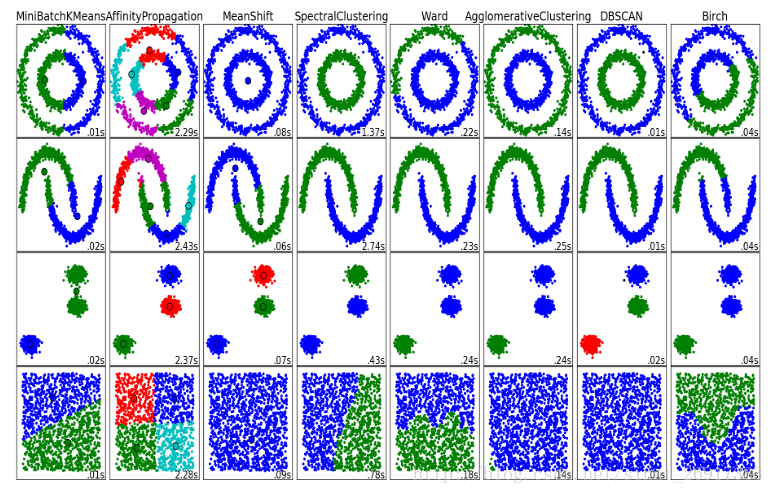
对比
对比图:
一般用于数据集稠密时的情况,或数据集是非凸的。
DBSCAN的主要优点有:
- 可以对任意形状的稠密数据集进行聚类,相对的,K-Means之类的聚类算法一般只适用于凸数据集。
- 可以在聚类的同时发现异常点,对数据集中的异常点不敏感。
- 聚类结果没有偏倚,相对的,K-Means之类的聚类算法初始值对聚类结果有很大影响。
DBSCAN的主要缺点有:
- 如果样本集的密度不均匀、聚类间距差相差很大时,聚类质量较差,这时用DBSCAN聚类一般不适合。
- 如果样本集较大时,聚类收敛时间较长,此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。
- 调参相对于传统的K-Means之类的聚类算法稍复杂,主要需要对距离阈值ϵ,邻域样本数阈值MinPts联合调参,不同的参数组合对最后的聚类效果有较大影响。
sklearn.cluster.DBSCAN
参数
按其算法,包括DBSCAN本身的参数,以及求取最近邻时的参数。
- eps:DBSCAN算法参数,ϵ-邻域的距离阈值。默认值是0.5.eps过大,则更多的点会落在核心对象的ϵ-邻域,此时我们的类别数可能会减少, 本来不应该是一类的样本也会被划为一类。反之则类别数可能会增大,本来是一类的样本却被划分开。
- min_samples:DBSCAN算法参数,上文的MinPts。默认值是5.通常和eps一起调参。在eps一定的情况下,min_samples过大,则核心对象会过少,此时簇内部分本来是一类的样本可能会被标为噪音点,类别数也会变多。反之min_samples过小的话,则会产生大量的核心对象,可能会导致类别数过少。
- metric:最近邻距离度量参数。可以使用的距离度量较多,一般来说DBSCAN使用默认的欧式距离(即p=2的闵可夫斯基距离)就可以满足我们的需求。可以使用的距离度量参数有:
- 欧式距离 “euclidean”
- 曼哈顿距离 “manhattan”
- 切比雪夫距离“chebyshev”
- 闵可夫斯基距离 “minkowski”
- 带权重闵可夫斯基距离 “wminkowski”
- 标准化欧式距离 “seuclidean”
- 马氏距离“mahalanobis”
- algorithm:最近邻搜索算法参数,算法一共有三种,第一种是蛮力实现,第二种是KD树实现,第三种是球树实现。对于这个参数,一共有4种可选输入,‘brute’对应第一种蛮力实现,‘kd_tree’对应第二种KD树实现,‘ball_tree’对应第三种的球树实现,‘auto’则会在上面三种算法中做权衡,选择一个拟合最好的最优算法。需要注意的是,如果输入样本特征是稀疏的时候,无论我们选择哪种算法,最后scikit-learn都会去用蛮力实现‘brute’。个人的经验,一般情况使用默认的 ‘auto’就够了。 如果数据量很大或者特征也很多,用”auto”建树时间可能会很长,效率不高,建议选择KD树实现‘kd_tree’,此时如果发现‘kd_tree’速度比较慢或者已经知道样本分布不是很均匀时,可以尝试用‘ball_tree’。而如果输入样本是稀疏的,无论你选择哪个算法最后实际运行的都是‘brute’。
- leaf_size:最近邻搜索算法参数,为使用KD树或者球树时, 停止建子树的叶子节点数量的阈值。这个值越小,则生成的KD树或者球树就越大,层数越深,建树时间越长,反之,则生成的KD树或者球树会小,层数较浅,建树时间较短。默认是30. 因为这个值一般只影响算法的运行速度和使用内存大小,因此一般情况下可以不管它。
- p: 最近邻距离度量参数。只用于闵可夫斯基距离和带权重闵可夫斯基距离中p值的选择,p=1为曼哈顿距离, p=2为欧式距离。如果使用默认的欧式距离不需要管这个参数。
- n_jobs:使用CPU格式,-1代表全开。
输出:
- coresample_indices:核心样本指数。(此参数在代码中有详细的解释)
- labels_:数据集中每个点的集合标签给,噪声点标签为-1。
- components_ :核心样本的副本
主要是eps和min_samples的调参。
代码实例
原文2中有。
原文2